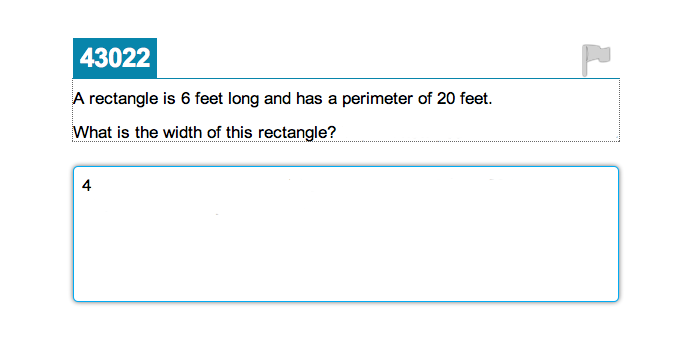
Here is a released question from Smarter Balanced (I even answered it!!!):
Ok I lied. That was an edited version of a Smarter Balanced question – here’s the original:
Now all of a sudden my answer doesn’t seem sufficient anymore 🙁 Here’s my best guess at a popular student answer:
This word “explain” is keeping me up at night lately. In this problem I’m not sure adding the word explain to the end gains us enough to warrant it. To achieve Common Core we can’t just throw the word “explain” after every problem we did last year and call it a day. By the way I’m not saying that’s what the Smarter Balanced Consortium did on this particular problem. But this use of the word “explain” does bring two things to mind:
1. It’s hard to explain your mathematical reasoning without access to drawing diagrams.
2. If we ask students to explain something – it should be something worth explaining.
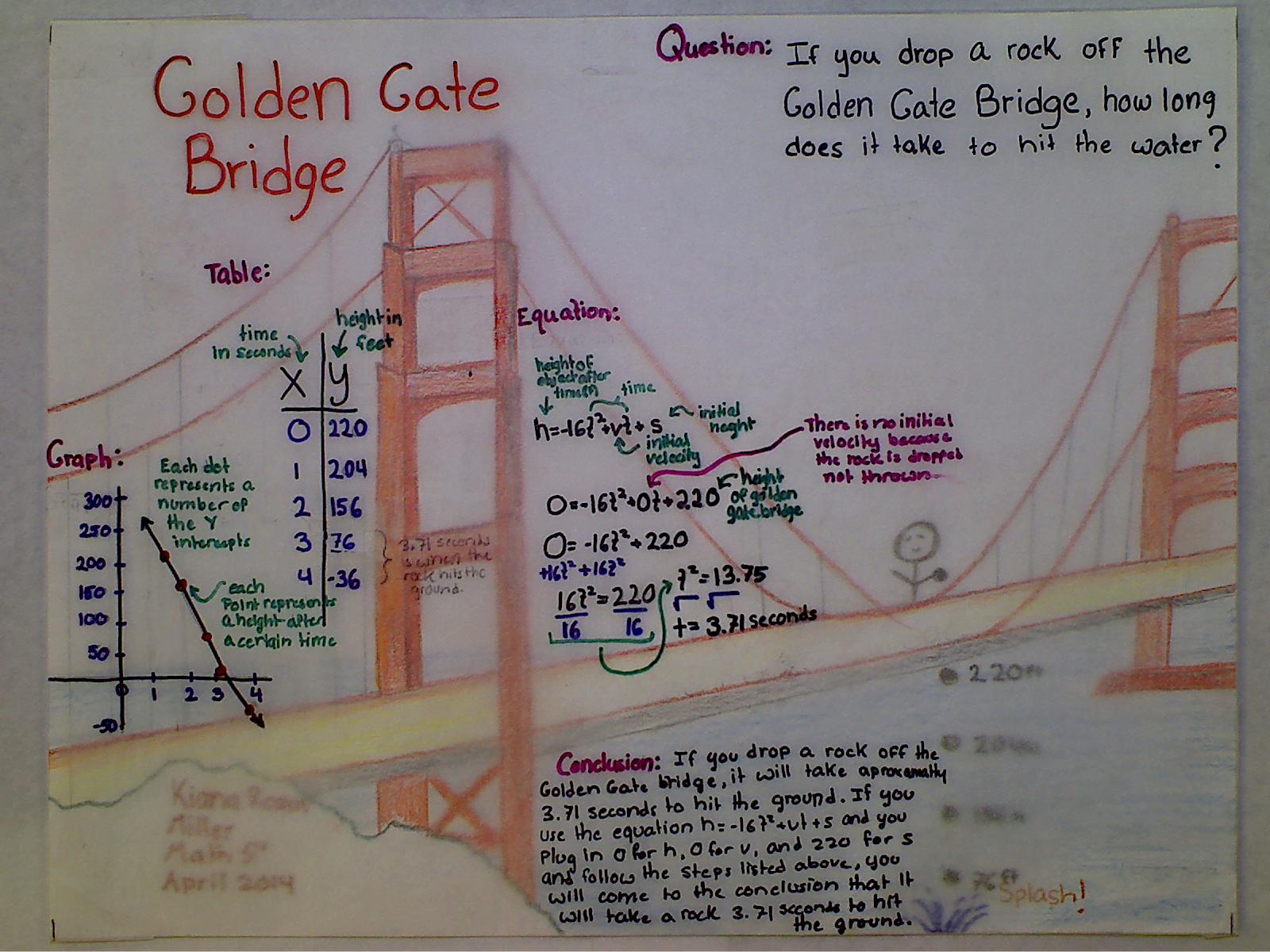
With respect to #1 – my focus this year has been on explanations through multiple representations. Basically I have students make connections between diagrams, tables, graphs, mathematical symbols, and written descriptions. I feel underwhelmed asking students to explain with just a typed explanation. I want explanations to look like this:
In the student work above – image if it was only the conclusion. Look at how much would be lost.
There are certainly better answers to the rectangle problem from Smarter Balanced than I offered up here. I actually really like the problem itself, I just do not think having them explain it gains us much versus just solving it.
It’s hard to explain the word explain. It’s a word that only makes sense to me until I try to explain it.
