This lesson could be better – but it was my first shot at it. I still definitely recommend it because of the great math conversations we had around convenience and adding value. Here’s the driving question I used:
What is Convenience Worth?
But it didn’t work as well as I wanted it to because we were really only looking at the convenience of the k-cup vs. ground coffee vs. going to a coffee shop. It’s a cool driving question, but not necessarily the focus of this lesson. This lesson is based more on “adding value” – where value is defined as what people are willing to pay for. Starbucks added value to it’s coffee grounds by putting them into K-cups, and that is why they are able to charge more for it. So how much value did they add?
So here’s the lesson:
Angle 1: K-cups vs. Ground Coffee
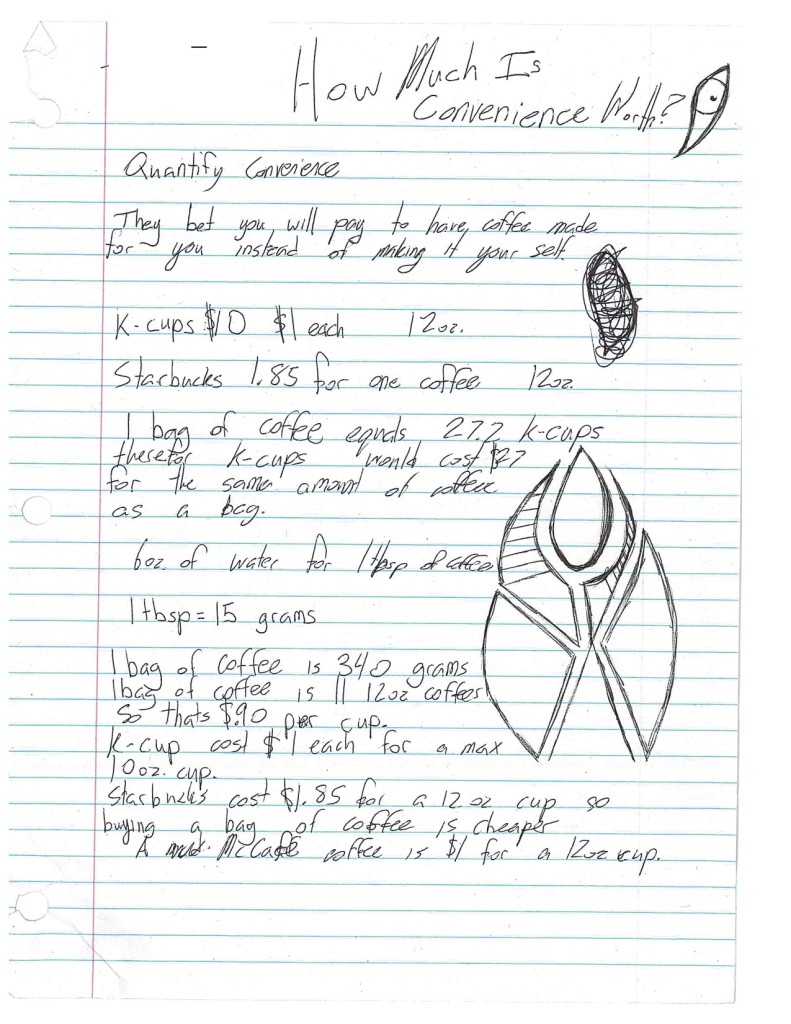
Starbucks makes K-cups and ground coffee, and both sell for $10! [excellent] So are they the same price? The K-cups are a package of 10, 12.5 gram cups. And the ground coffee is in a 340g bag. Starbucks is able to elevate it’s price for K-cups because they are more convenient than traditional brewing methods. So what’s the value of that convenience?
Angle 2: Coffee Shop vs. Brewing At Home
It is more expensive to buy a cup of coffee at Starbucks than it is to brew it at home. Yet people still do it. What does that cost difference tell us about the value of convenience? Here’s one of Starbucks menus:
There was definitely a period at the beginning where students did not know how to begin – or perhaps what they were suppose to do. It took some time for them, and to extent me as well. to define the question. I told them that it is natural in any problem solving situation to spend time defining the question, framing assumptions, setting up your analysis.
My teacher moves were as follows:
– Write about a time when you paid extra for convenience. Talk it out.
– Ok so the value of convenience depends on how convenient the thing is versus the alternative. [Future project could be to quantify convenience itself, rather than only focusing on Starbucks pricing]. That means we should standardize the convenience we are analyzing. So let’s look at convenience through the lens of Starbucks pricing.
– What does the pricing of Starbucks coffee tell us about the value of convenience? How could we use Starbucks to quantify its convenience. What information would we need?
– Give various pricing data
– Ask students to come up with a value for the convenience of the k-cup vs. ground coffee, or the value of going to Starbucks versus brewing at home.
– Helping individually. My most effective question was “For $10 you get 340g of ground coffee. How much would it cost to get 340g of coffee in K-cups?”
It is also an interesting conversation that ground coffee and whole bean are the exact same price. So Starbucks is saying that the convenience of having the beans ground for you adds no value to the product.
After the activity we read an article from Proffer Brainchild titled “ADDING VALUE: A Lesson From Starbucks”
Here are some examples of student work. The first example was the highest quality paper I received.
Lesson Learned:
It’s clear that not all students understood what I was asking – and so I concede that “What’s the value of Convenience?” was not a good driving question for this particular activity. I do see it that prompt as a great math modeling problem where students try to quantify an inherently qualitative thing. But that’s not what they were doing here.
Next year I am going to try and focus first on the k-cup vs. ground coffee prices and stick the economics concept of “adding value”. How much value is added when Starbucks puts their grounds in K-cups vs. ground coffee? And this is not just about the calculations, it’s about the argument.