I ended up having this go over two days and looking back I’m very glad I did. Here are my notes for day one of the lesson which is where they folded the model. For specific folding instructions – go over to georigami.com and watch Dave and I fold the duck. I recommend watching the “For Educators” video.
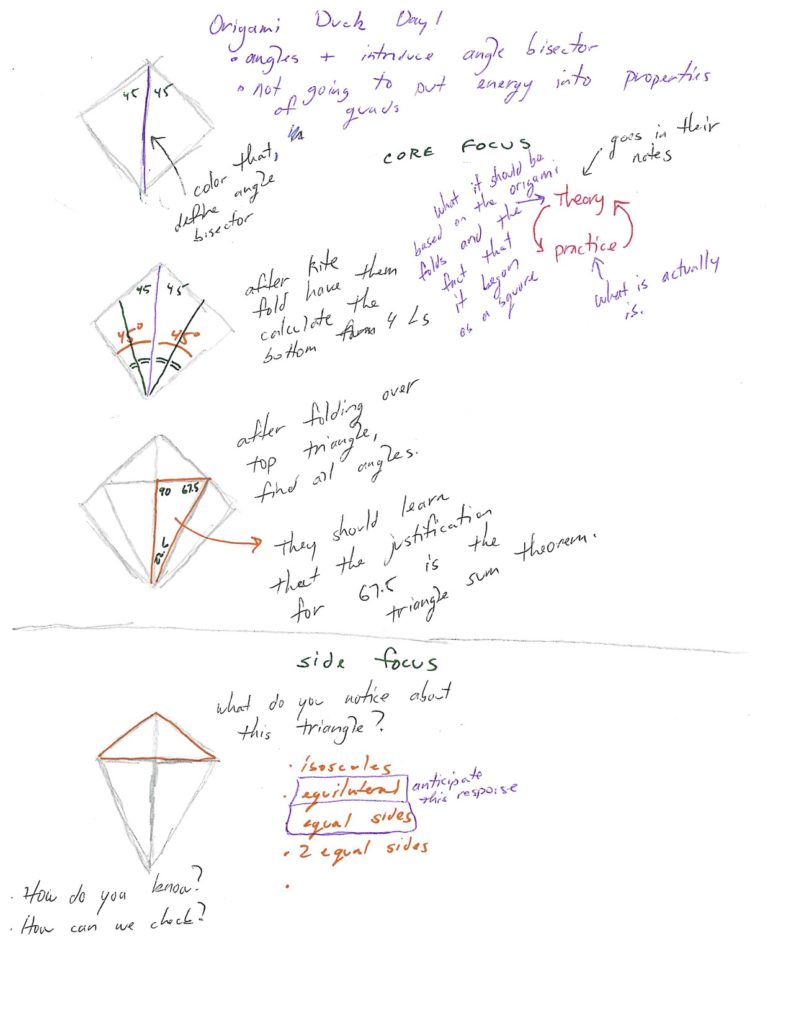
When I write out my plan I like to be very direct my main focus – but I also note any questions I want to pause on that aren’t part of my main content goal. So in this case – my main goal is the angle bisector and angle measures, but you can see I have carved out a specific time when I am going to deviate from that and do a ‘what do you notice’ on the step when they first fold the kite.
Day 1: Fold the duck and find all missing angles. Not worrying about having to provide justifications (warrants) and notation. I focus on introducing the angle bisector because ultimately they are going to be solving for angles and almost each one is specifically related to a bisecting.
As I show in my notes – I did pause after each bisecting and had them figure out what the resulting angles were and mark the angles as congruent directly on their origami model.
I gave them individual time to figure out the angles right there on the origami model. Then I grouped them and they went to whiteboards, drew the model on the board and solved it in teams. I had a couple of the folding patterns printed out to help them draw it. Just drawing the fold patterns is a lesson in itself since they have to draw the best square they can, and then attempt to properly bisect the angle. To draw a bisector you must understand a bisector.
I intentionally used the folding pattern without labels because I didn’t want anything to distract from figuring out what every angle was. But I suppose you could label it with points.
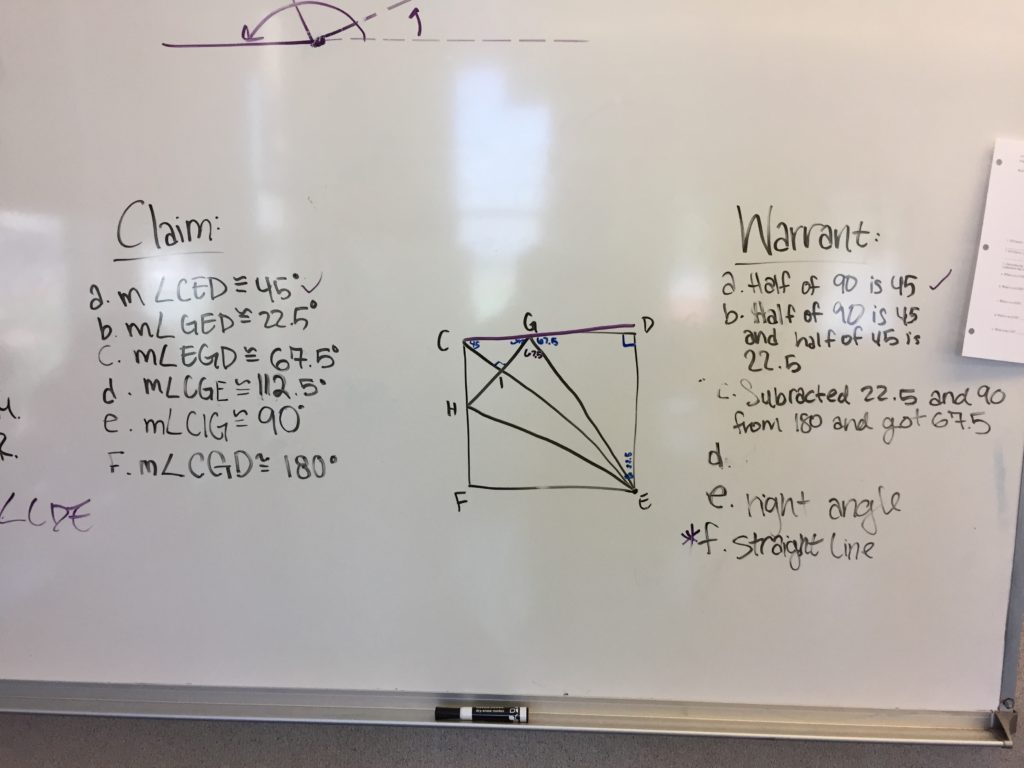
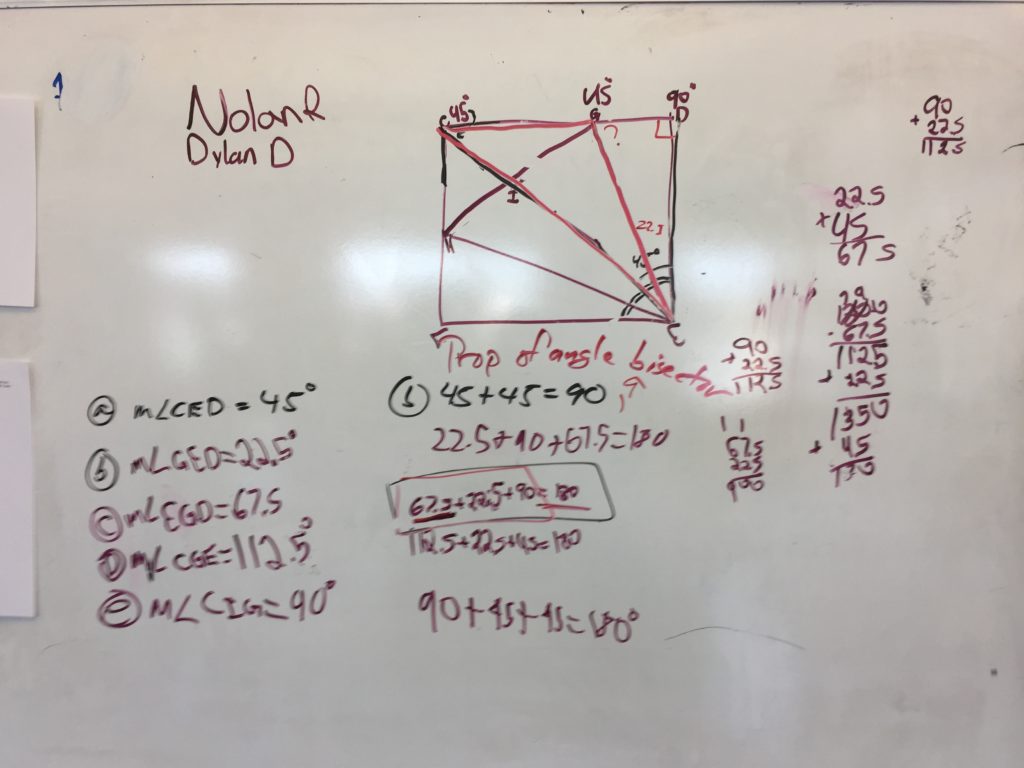
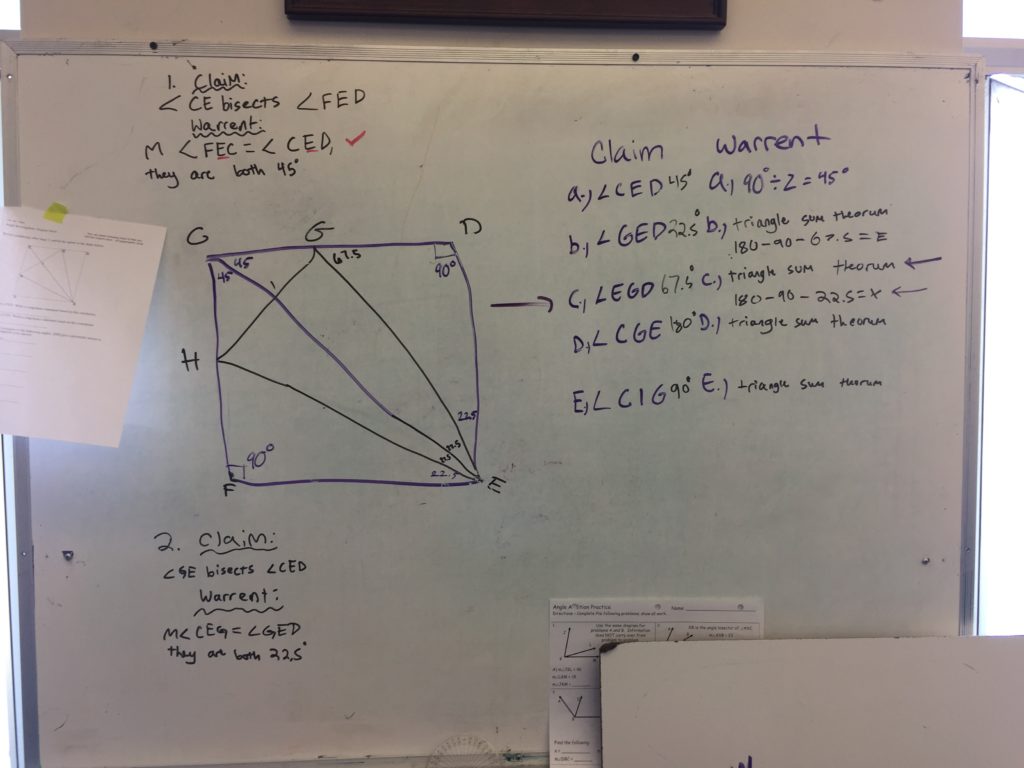
Day 2: No folding, they just completed the Origami Duck worksheet. I had them do it all at whiteboards, but having them work it on paper is cool too. The idea is that now they are using proper notation, and needing to provide warrants for each claim (unlike day 1). I used the worksheet from georigami. I added the structure of CLAIM/WARRANT because that is the language we are using this year.
The reason I broke it into two days is because this is the 4th day of the year and I didn’t want the structure of CLAIM/WARRANT or the notation of defining angles to get in the way of their conversations about the value of each angle. The second day they needed to find specific angles called out in the worksheet, and format it in a two column style with CLAIM / WARRANT.
ORCHESTRATING THE END OF THE CLASS
My goal at the end of the 2nd day is to take the students around the tour of the room and look at the justifications. I am looking for a group whose warrants are only the algebra steps they used. Then I’m looking for a group who might have described what they did in words – “we cut the 45 degree angle in half”. I would like to find a group that justified their responses with theorems (property of a bisector, triangle sum theorem) but didn’t show algebraic steps. And lastly a group that did both – like one of the ones pictured below.
For me this is early in the year, so while the students are working I’m letting them take the word “warrant” and have it mean whatever they want. My goal is for them to walk away with this distinction in mind:
Is it one thing to say the reason the angle is 67.5 is because 180-90-22.5 = 67.5. But why does that algebra produce the correct answer? What do you say to the person who doesn’t understand what gives you the right to do that? You need to do more than just show the algebra, you must quote the theorem that supports the steps.
Or put in less words
Oh, I need to justify my algebra steps.
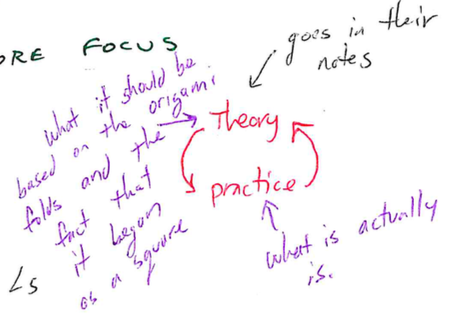
THEORY VS. PRACTICE
You might have notice this diagram in my notes above:
I have them put it in their notes. It’s fundamental to my origami lessons. Here’s why: When you ask students to find the angles – is measuring the angles good enough? My speech is that “theory” is what the angles should be – given that we started with a perfect square and did each origami fold perfectly. They need to calculate angles based on “theory”. Then I have them check their calculations by measuring what the angles actually are, which is the “practice”. “There is always error in measurement” as Dave says. So I don’t want them telling me their measurements and theory are identical.
At the end of the day the theory informs the practice and the practice informs the theory. For example with the duck – the students might decide that on of those four congruent angles is 45 degrees. But when they measure it they notice it is actually more like 22 degrees. The reality of the angle provides insight into their calculation that they are not taking into consideration a bisector.
FOLDING HEADS UP
I didn’t pre-fold any models. The duck is the first model I do and it has three inside reverse folds – so just be aware that they will find those difficult. If I was to pre-fold I would pre-fold 8 models to where the neck is done but not the head.
Ok – that’s it. It’s just a duck afterall.
Cheers!
– B