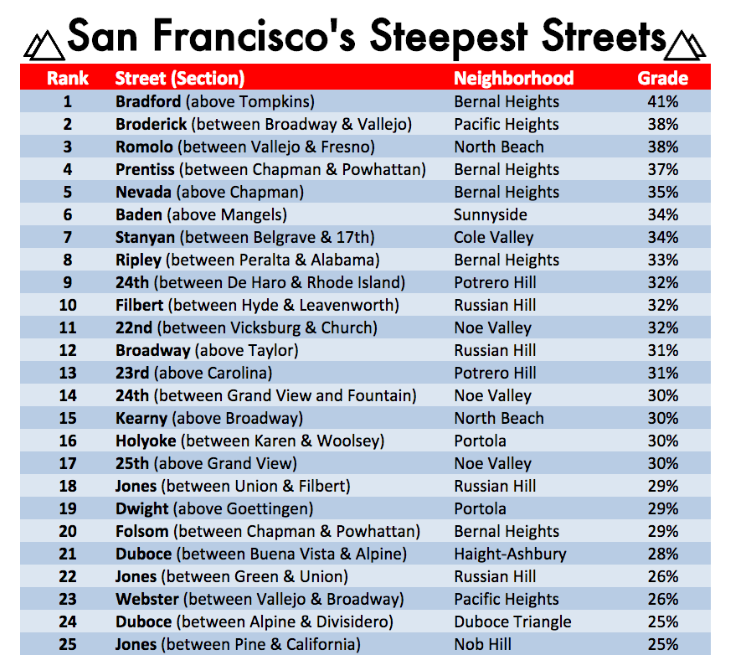
Here’s a post regarding the My Favorite I did at TMC16 on how I used the Mathalicious lesson “Licensed To Ill” to have a conversation that mattered. And since Karim inspired me to go this way with his blog post On Purpose – I’ll defer to him for the reminder about why it’s important:
@cmmteach @TheMillerMath As a species, we’ve had a rough last few weeks, huh? We need to be able to have these conversations more than ever.
— Karim Kai Ani (@karimkai) July 18, 2016
The video of the presentation is here: (Thanks Glen!)
I’m going to highlight what changes I made from the suggested lesson delivery. Go to the Mathalicious website for the specifics of the lesson. I took the pulse of the room and a lot of students had opinions about health insurance and Obama care but did not understand what it was or know any of the details. Mathalicious provides a great video introduction to health care that allowed me to make sure every student had a basic idea of it before going into the scenarios outlined in the lesson.
The most effective thing I added to Mathalicious lesson was the physical simulation. There was a story telling benefit, a pedagogical benefit, and a mathematical benefit:
- Allowed me to increase the drama around denying Daniel.
- Anytime you put something in the students hands it is a win.
- We got to use all the simulation data to better discuss it’s relationship to the expected value.
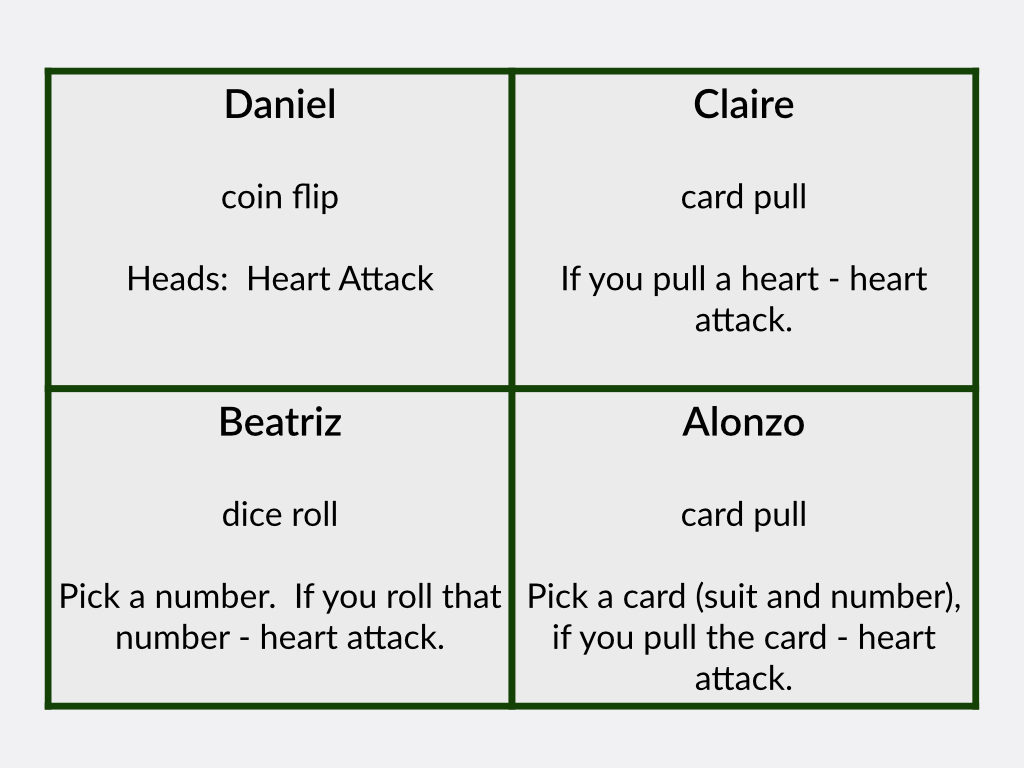
I think there could be a cool teacher move where the students come up with how to simulate these probabilities, but I choose to have that all setup from the start. I made sure the room was setup a bit different than normal, and each table already had a decks of cards, a coin, and dice.
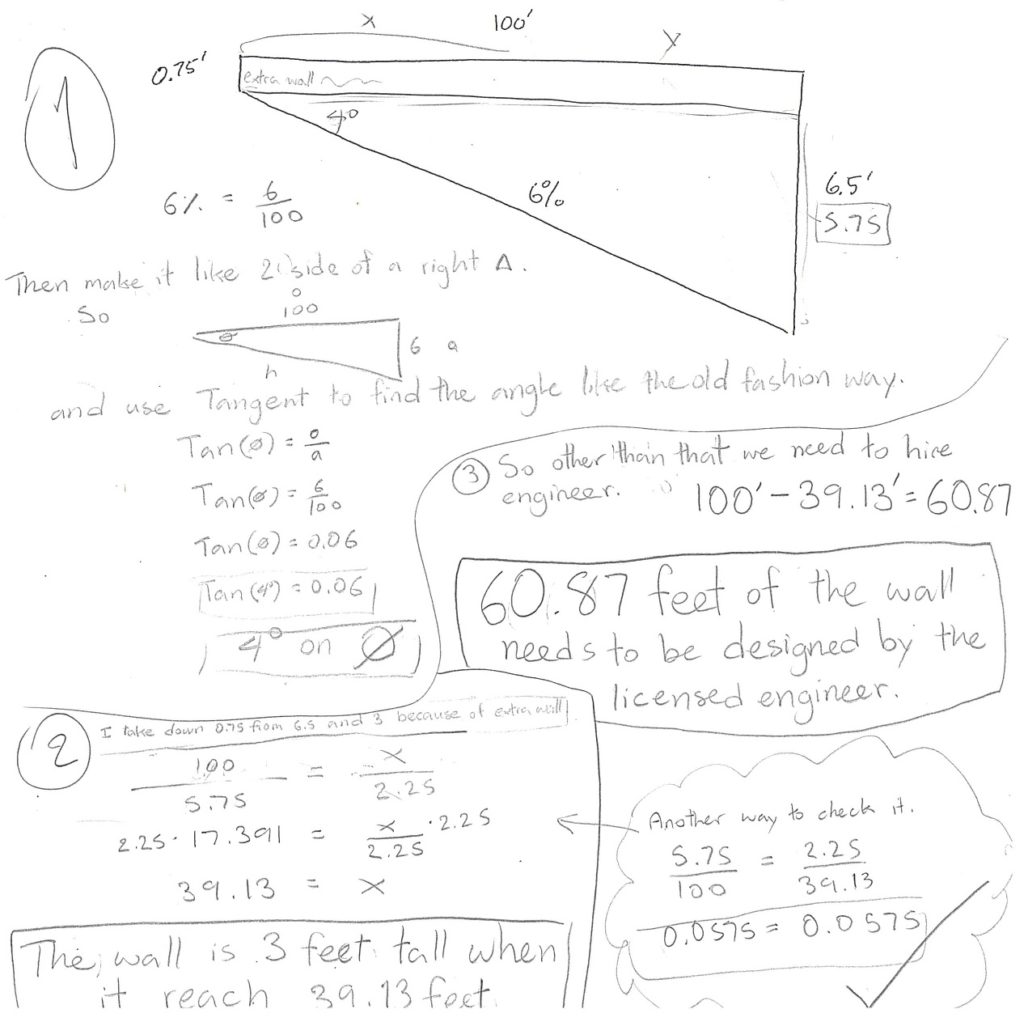
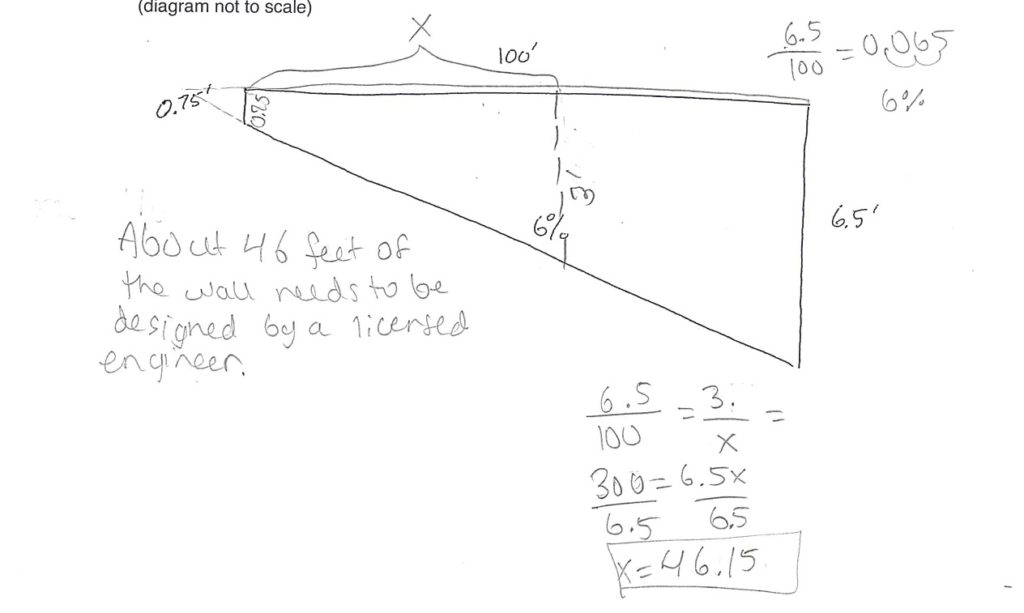
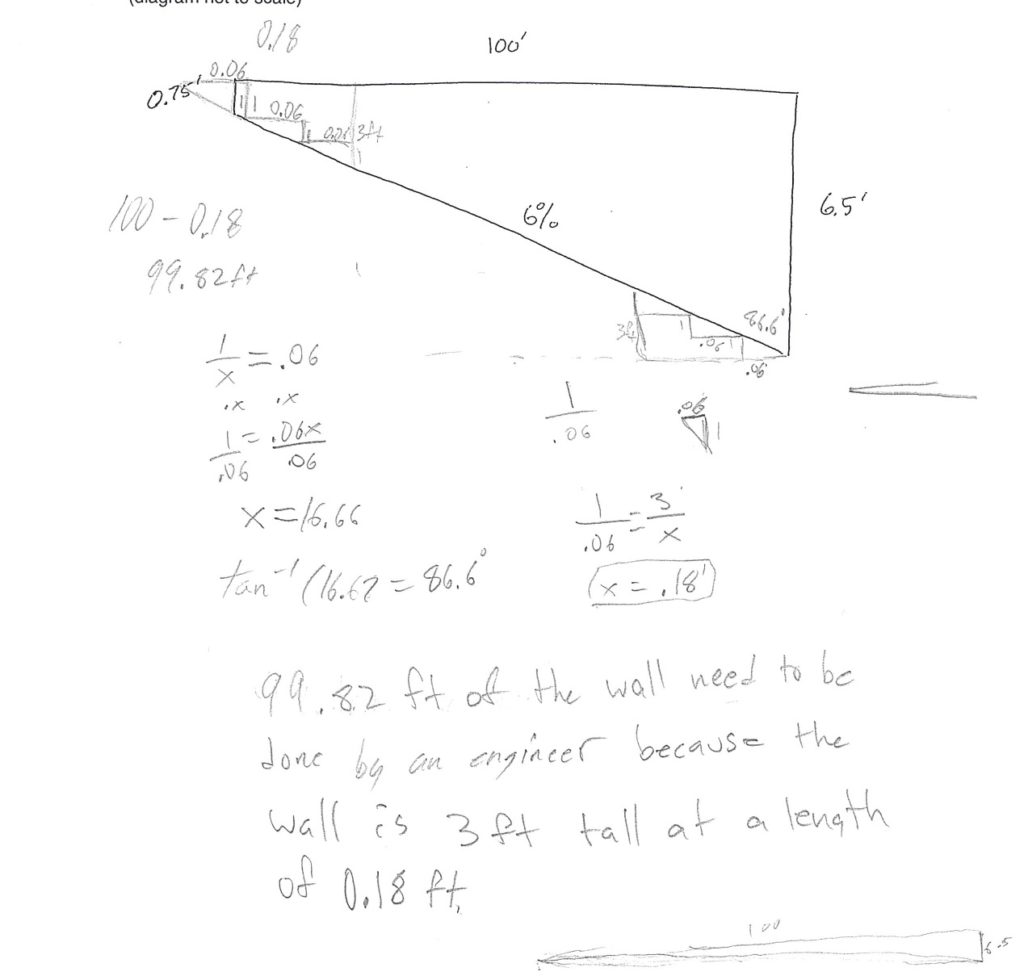
Alonzo’s probability on the card draw isn’t 1%, so I talked to the students about whether or not we thought it was sufficiently improbable for our purposes. My student teacher said we could have them draw from a 50 card deck, and then if they draw correctly then they flip a coin. I thought that was cool – but the idea came after we had already started so I didn’t go with it.
I did have the students keep a record of all their simulations, which allowed us at the end to compare our expected values with the results of all our simulations. This is particularly helpful in the “set your price scenario” where they expect a profit of $0, but the only possible results with a single Daniel is +/-$20,000.
One edit I did which was subtle and only done for storytelling purposes was to make the students the insurance company. You can make the story more interesting to students by injecting them into it. Now instead of asking the students to calculate the expected profit of the insurance company, I would instead ask “calculate your expected profit”.
Although I did most the work at VNPS – I did do the reflection portion on the videos with the exact same handout Mathalicious gives.
Here’s the final grid. I started with just two columns and had the students add a column with every new situation. That way they didn’t know how many we were going to do and it kept the direction of the lesson more surprising.
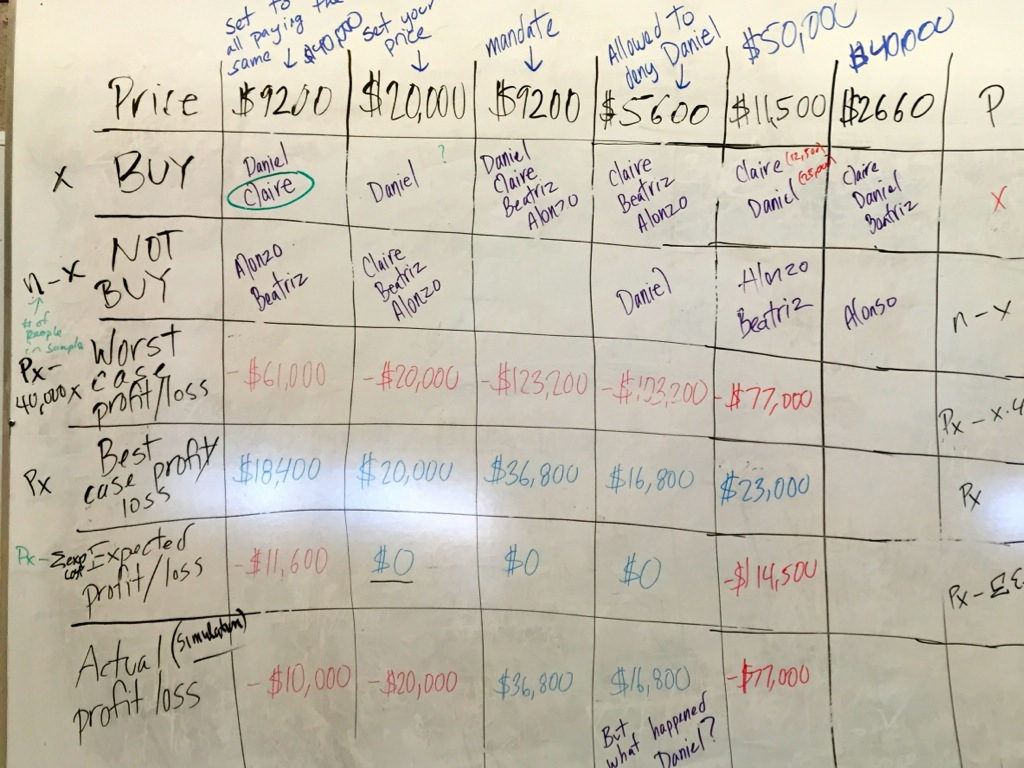
Out of all the scenarios, the only one I actually added was the generalization at the end. I also changed the instruction on the second scenario – preferring to have them “set their own price” to try and fix the problem from the first scenario. Mathalicious is more explicit with their instruction.
I am asking students to figure out the profit for the best and worst case scenarios. I’m undecided if this actually provides them insight into the situation and I’m mostly doing it because I want to ask them to calculate the probability of the best and worst case scenario which will allow me to see if they are adding or multiplying probabilities.
In the moment of giving the lesson I would periodically put the mandate in effect. For instance, when you can deny Daniel I told the kids to have Alonzo buy. Sometimes the mandate was still in effect, other times it was more a better safe than sorry thing. Once the mandate is first introduced, the students wanted to know if it was in effect for each of the subsequent scenarios.
The questions I keep repeating over and over again are “what are the advantages and disadvantages?”, “who wins, who losses?”, “Is this fair to _______ “, “Do you agree with… “.
The Conversation That Matters:
I frame each scenario to the students pretty much like I did in the video. I had to skip a few elements of each scenario in my TMC presentation in order to make the 10 minute window.
The mathematics has to better inform the students of how heath care works, and how changing specific parameters effects the situation as a whole. I am not trying to tell students that the Mandate is fair or unfair for Alonso, or that it’s fair or unfair to deny Daniel coverage just because he is likely to have a heart attack. I am trying to give them a sense of how insurance works, and to look at how changing certain parameters effects other parameters – sometimes in positive ways, other times in negative ways. Then I want that understanding to then form the basis for an informed opinion of “fairness” and ultimately whether or not something is a good idea.
Here’s some more of the slides from my presentation.
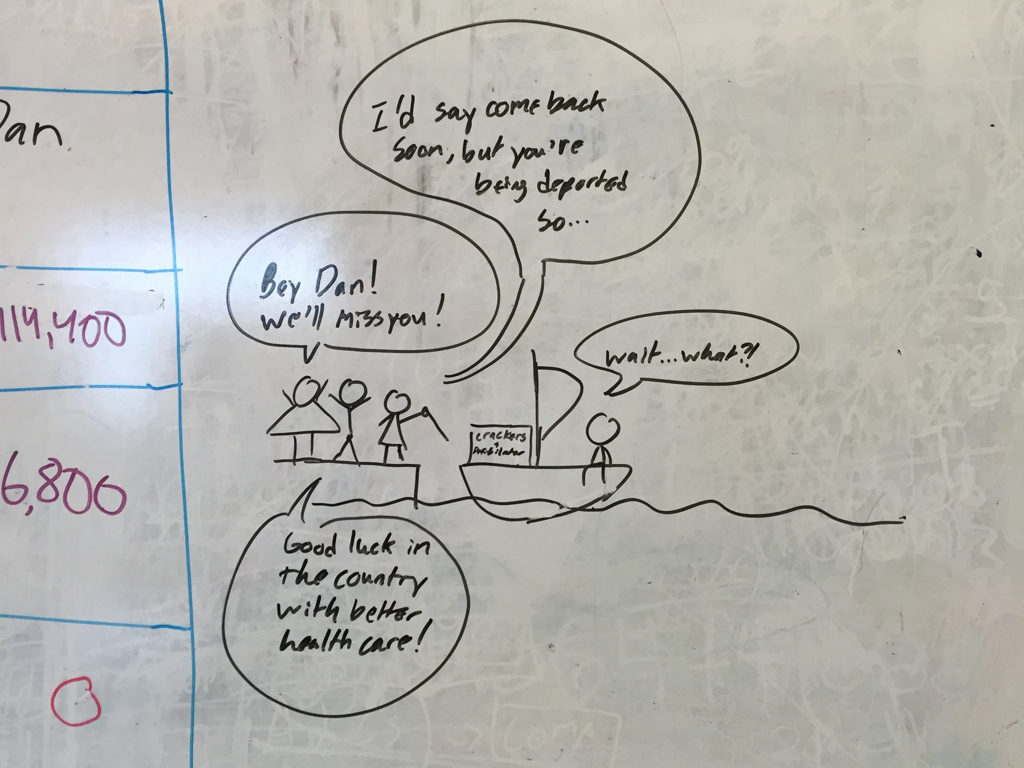
And here’s the comic that a girl drew up on her whiteboard after we went through the scenario of denying Daniel health care for his pre-existing condition: