Tag Archives: open middle

“Real-Life” Annulus Problem!

Posted on June 8, 2015 | 1 comment

I just can’t type “real-life” without quotes because I’m yet to resolve what “real-life” means in a math class.  But for this post it means – “Math someone needed to do at their job”.  And in this post that someone is my wife – who much to her distain and my joy – does a lot of geometry as a project manager at a construction firm.

So here’s what we need to know:  How much cement is needed to make that border?  We need the answer in cubic yards because you buy cement in cubic yards.

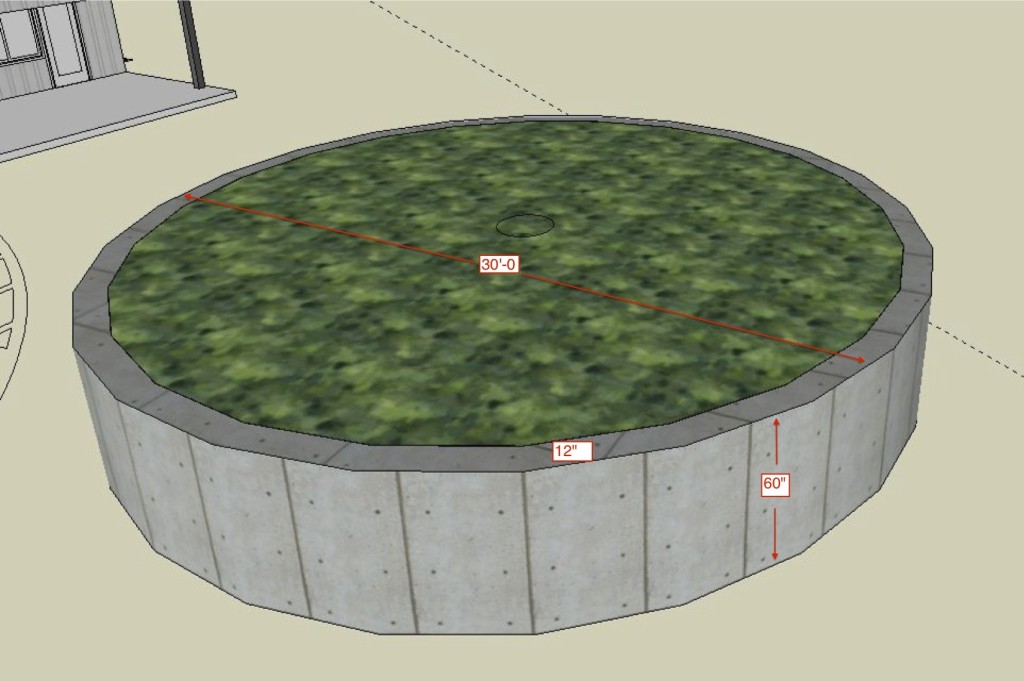
Concrete

The image below provides some of the context for the problem – The cement border is being used to circle an existing tree.

Freeman_2015-05-15_02

I was actually surprised how open the middle was on this problem.  Yet students used two main strategies.  The first was the standard subtract the areas and multiply by the height, or they subtracted the volumes of both cylinders directly.  The second was the find the perimeter, think of the wall as a rectangle (dimensions of 2*pi*r X 1′), find the area of that rectangle and then multiply by the height.

One student using the second strategy used a radius of 14ft and got a solution of 16.2 cubic yards.  He told me he knew the answer would be a little too small because of only using the inner radius.  Another students used 14.5 and got the same solution as the area subtracting syndicate.

Converting from cubic feet to cubic yards is a great time to practice your perplexed I wonder why you divide by 27? face.

By the way the wall ended up costing around $35000.  I can’t believe how long I would have to work to put a wall around a tree 🙁

Cheers!

– B

 

1 Comment

Posted in #industry, #technology, geometry

Tagged , , , , , , , , , ,

Standard Form Equations With An Open Middle

Posted on December 8, 2014 | 2 comments

#CMCN14 was lights out good this year.  Amongst the many things I learned new – were a ton of reminders of things that I used to think about but had let slip.  One of those things was the importance of an open middle, where students have a defined beginning and ending, but how they get there is largely up to them.   During Dan Meyer’s talk he challenged us to find an open middle in the routine, procedural fluency building exercises students get.  Most of the great problems have it – but it is a nice tool for tipping the scale for our procedural problems towards a deeper understanding.

Here’s the typical – pretty much closed middle – version of a problem about standard form:

Find the slope, y-intercept, and x-intercept of the following equation in standard form:  3x – 4y = 20

Here’s my one up

Write the equation of a line in standard form where the both intercepts are integers, and the slope is a fraction.

We could really be here all day playing with these

Write the equation of a line in standard form where the x-intercept is a fraction, the y-intercept is 7, and the slope is a negative fraction.

We can even get at MP3

Explain why it is not possible for the slope and x-intercept of a line to be an integer, but the y-intercept a fraction.

Lastly – the Asilomar conference grounds are so amazingly beautiful.  Each tree, slightly beaten from the ocean breeze, stand in stillness as perfect landmarks to perseverance.  And as the sun begins to set, and that air begins to cool, and those stars begin to show – it’s hard to believe that it’s all just the backdrop to a professional development experience.  It’s humbling to be there – I mean you’re walking from presentation to presentation with a program booklet offering the intellects and energies of 200 amazing educators.   But you only get to pick 5…  good luck with that.

2 Comments

Posted in algebra

Tagged , , ,