Keeping to my simple TMC15 definition of “Real World” as being math that someone needed to do at their job – I love this one. I believe these types of math problems deserve to be a spice in our curriculum. Especially in a geometry class! I used this problem at the end of Math 2 because it does a nice job of connecting angle measure and slope. I used it on an exam, so I will also show the two scaffolds I used.
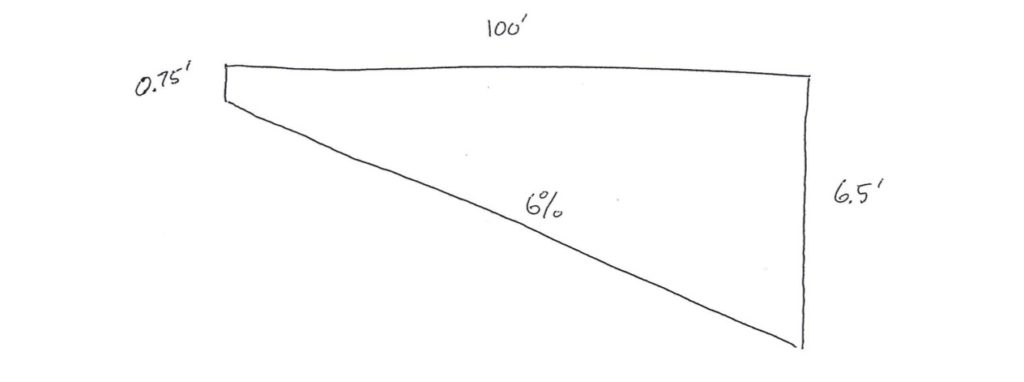
Basically my wife is building a giant barn / man cave and they need to construct a retaining wall. Here is how my wife explained the problem, and how I gave it to students. I gave them the below diagram as well. Too see how she delivered the question to me take a look at the text message at the bottom of this post.
Here’s how my wife wrote it:
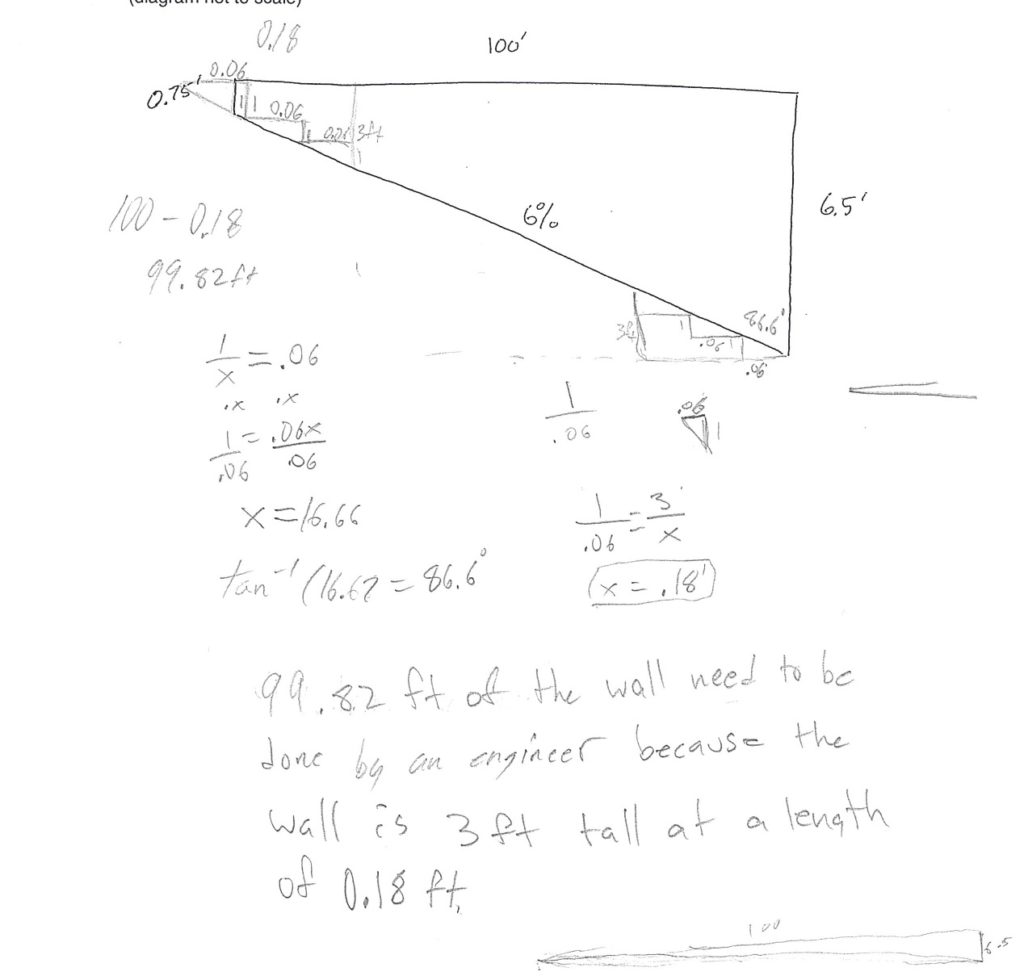
A General Contractor is building a retaining wall in Sonoma County. The General Contractor is required to have the portion of the retaining wall which is over 3’ tall designed by a licensed engineer. The base of the wall follows a driveway at a 6% slope. The top of the wall is level. How much of the wall needs to be engineered?
Here’s how I gave it to my students on their exam last year:
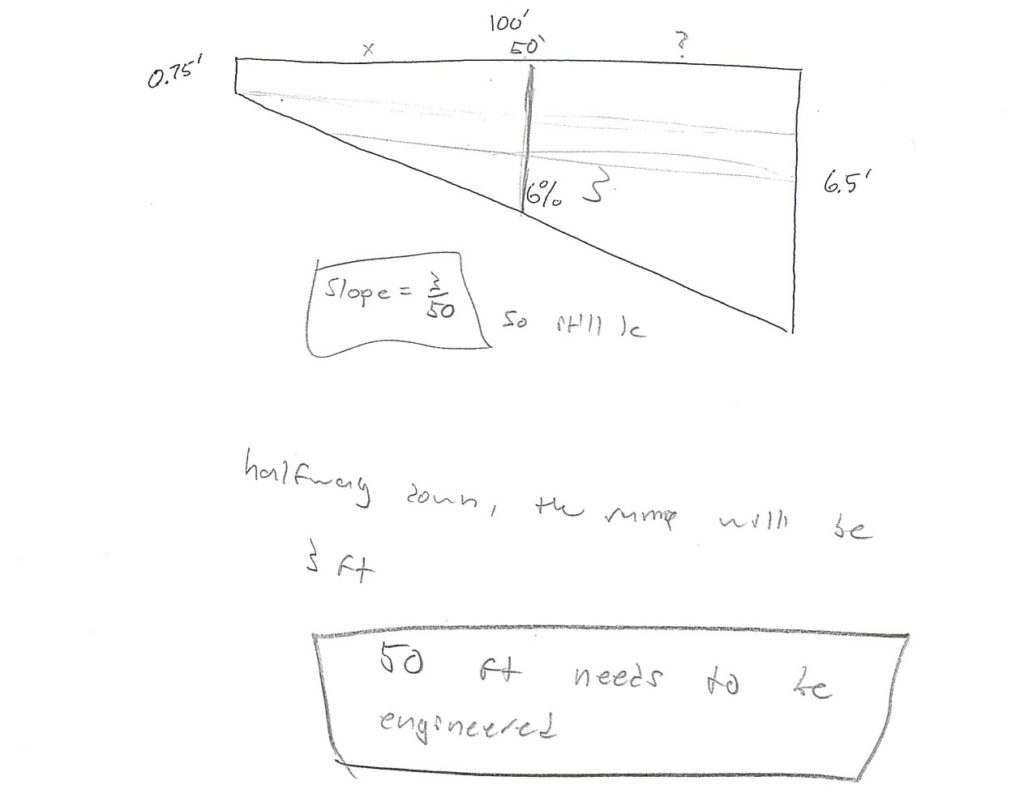
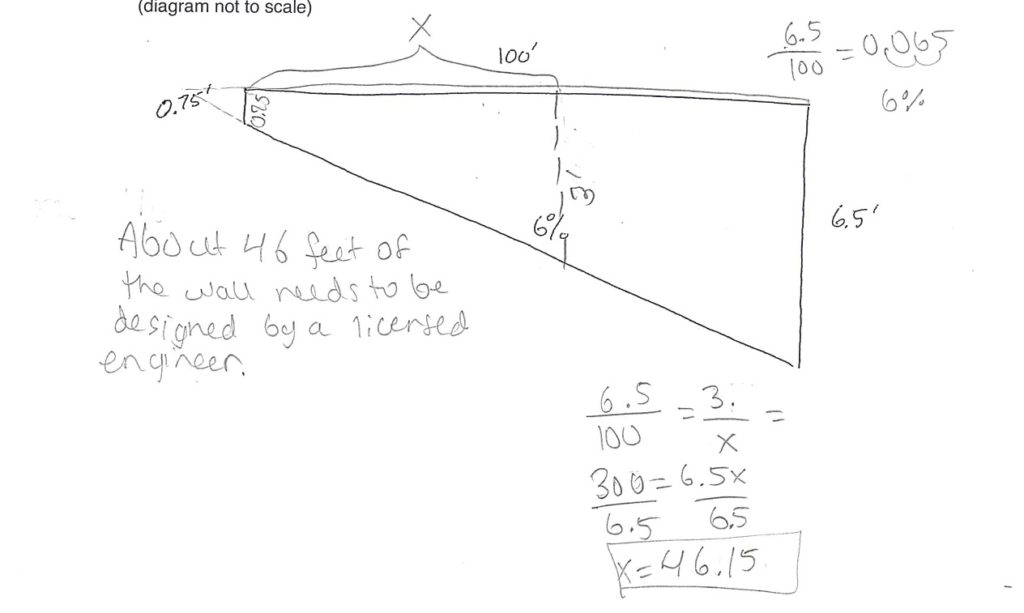
A General Contractor is building a retaining wall in Sonoma County. The General Contractor is required to have the portion of the retaining wall which is over 3’ tall designed by a licensed engineer. The base of the wall follows a driveway at a 6% slope. The top of the wall is level. The short side of the wall is 0.75 feet tall, and the tall side is 6.5 feet tall. How much of the wall needs to be designed by the licensed engineer? (Hint: When is the wall 3 feet tall?) (diagram not to scale)
I ended up loving this problem because it connected slope to angle measure, algebra to geometry. I got to tell them that in Math 1 we always talked about slope, but the angle measure was always there.
I used this problem as an exam question. In order to scaffold it I did the following two activities as openers. Both of them combined did a nice job of familiarizing the students with the language of the question. I also had gone over what a general contractor is before the exam.
Opener Scaffold #1
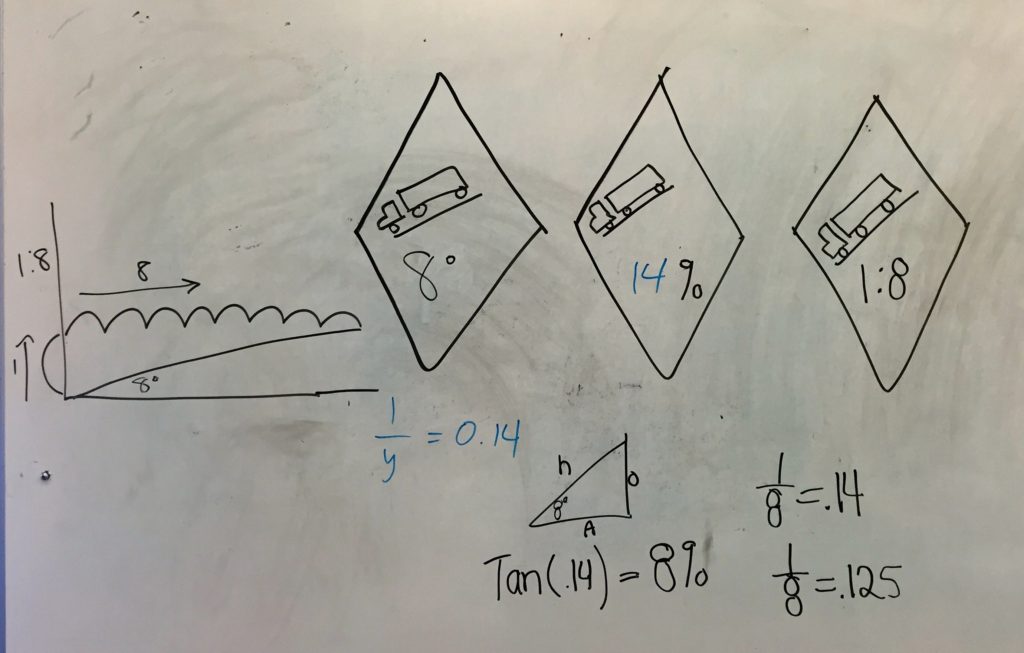
What would this road sign look like if we used slope or angle measures for gradients instead of grade? Draw all three. I didn’t run straight to this question – I developed it a bit first by asking questions like “what do you think this sign means?”.
Here’s an example of student work:
The point of this first activity was for students to become familiar with grades – the fact they are just the rise divided by the run in percent. Also I wanted to make the connection between slope and angle measurements, algebra and geometry.
For the question on the final I want them to have the ability to convert percent grade to an angle measure.
Opener Scaffold #2
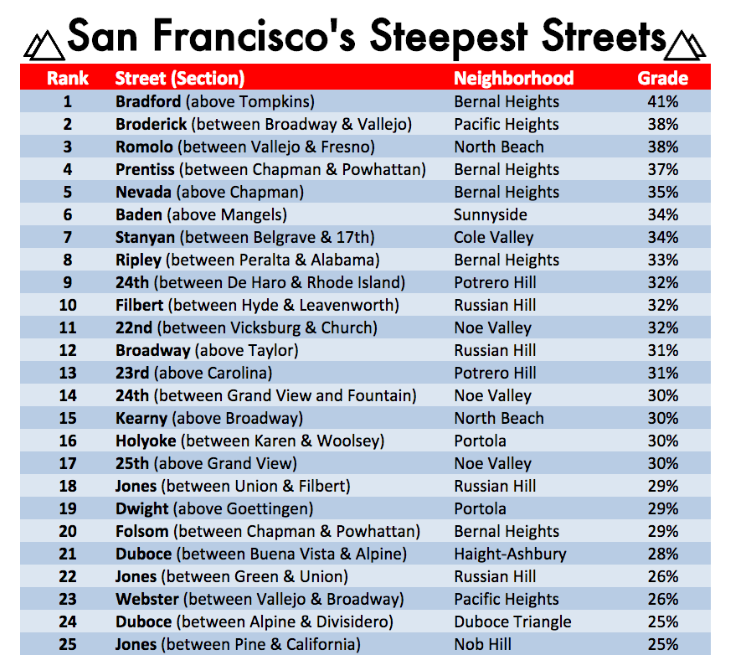
Pick two of these streets and draw a diagram of them using the angle measure instead of the percent grade. If you finish early build an accurate physical model of the street using string and tape.
This opener went well – I didn’t take any pictures.
Results:
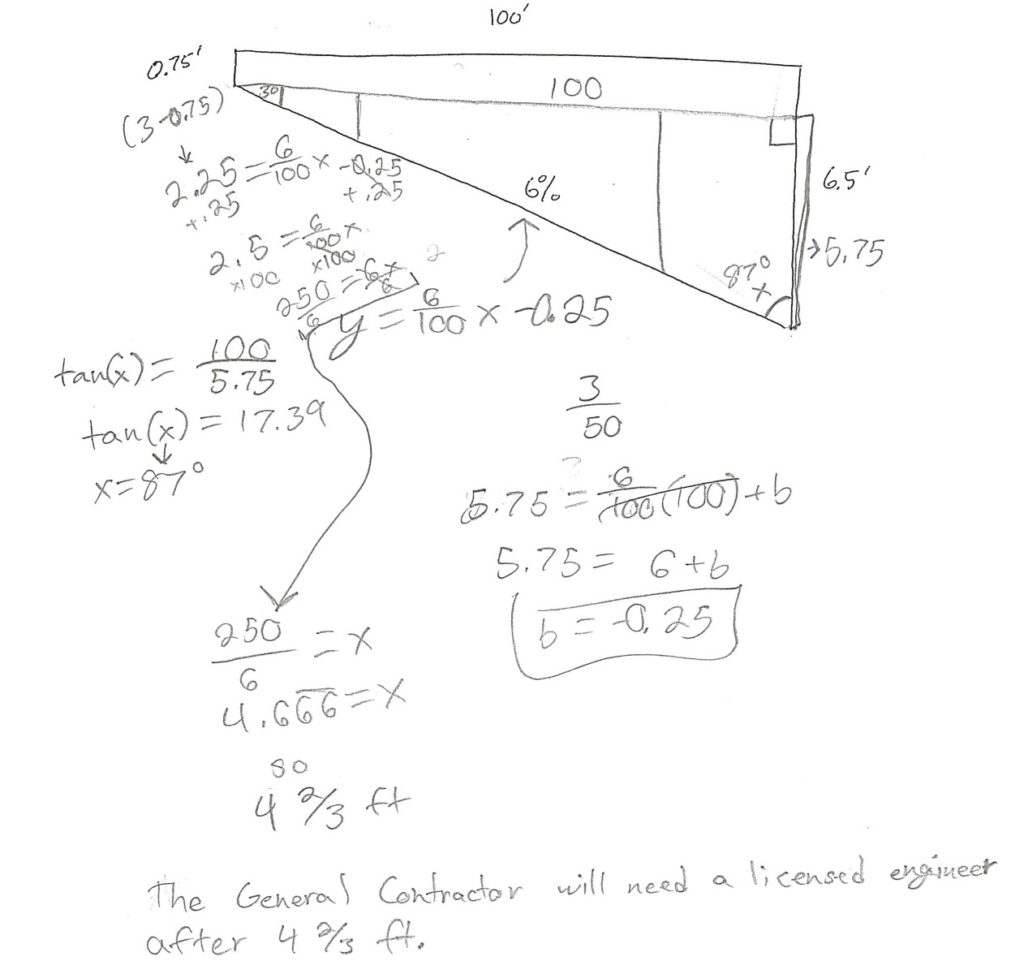
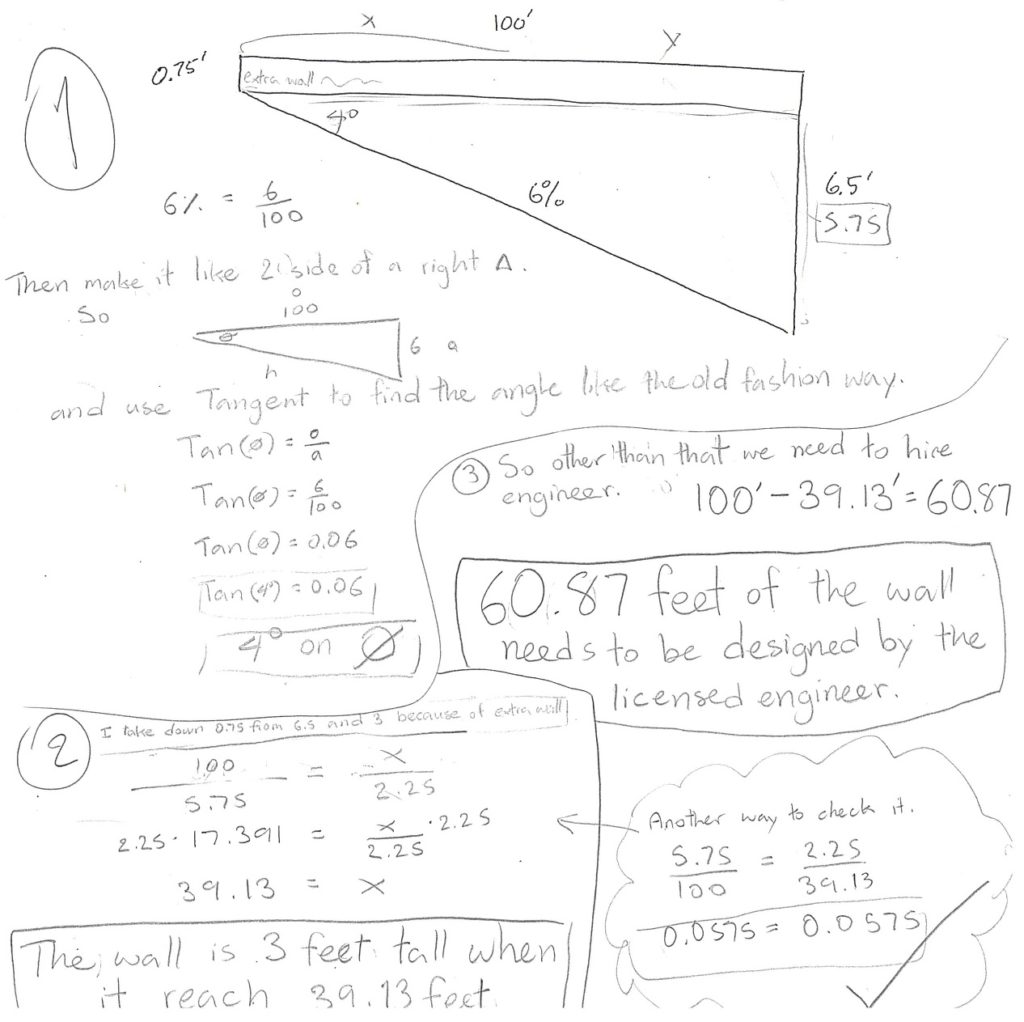
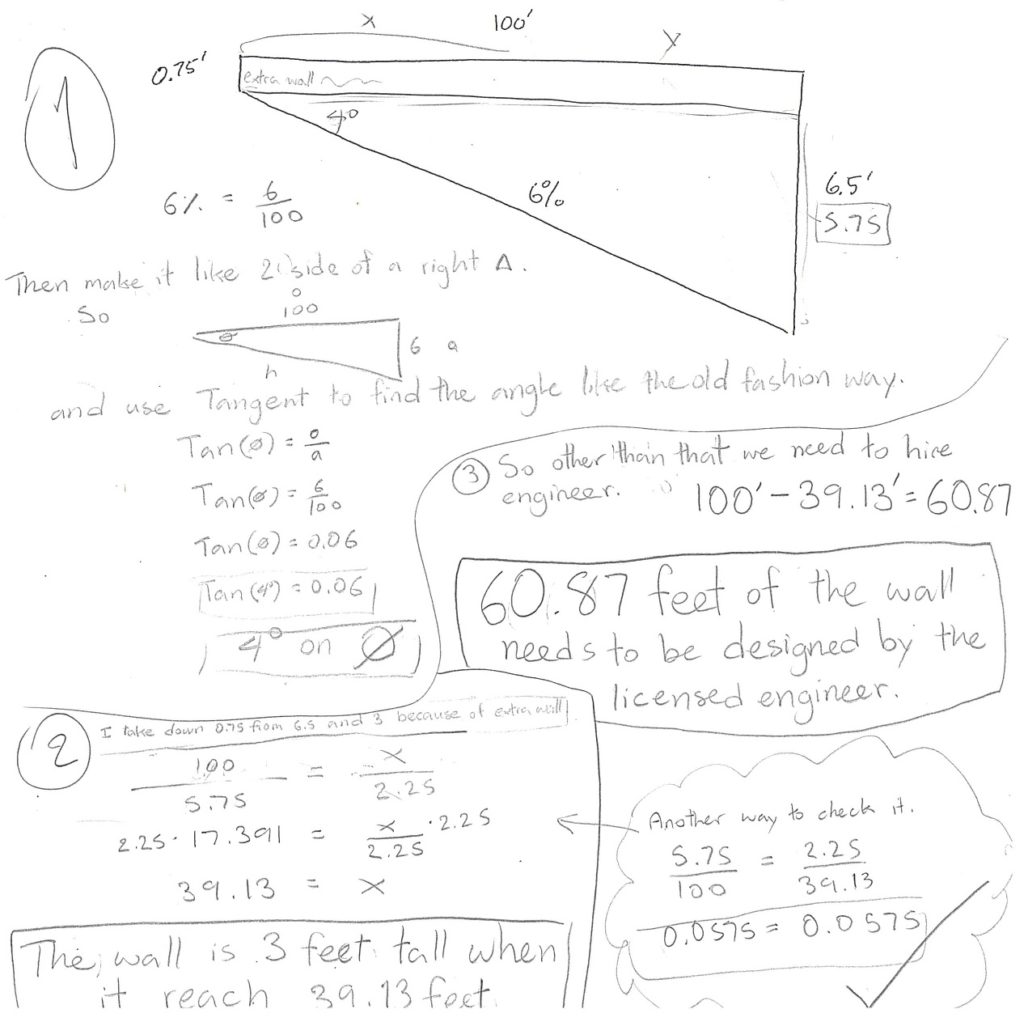
Here are some of the results of their work on the exam. I was surprised how many different ways the students went about solving it.
The Real Problem:
Here’s the actual text from my wife. Notice the dimensions she gave (0.8 and 6.56 ft) were different than the ones I used (0.75 and 6.5 ft). I changed the measurements because I didn’t feel I had done enough work with measurements for students to be able to deal with the actual dimensions. I still the question qualifies as real-world. Real enough world.
A Note On Construction Convention:
In construction – they would say “one over seven” to describe a slope of 1/7, and it would likely be written 1:7. A slope of 4/9 would be called “four over nine”. I talked about slope using that language during these activities.
The Goods: