I titled this “My Spiraling of Vroom Vroom” because I highlight how I used this lesson to teach (introduce) line of best fit and statistics. The original lesson uses line of best fit, but I also wanted to teach stats as well.
This would be the first time my students ever did a line of best fit and used it to make a prediction, and so I needed to add in some teaching around line of best fit. I also wanted to use the pull back cars for a lesson on mode, median, range, and mean – so I used a different day 1 activity. I’ll mention all the different “thinking” moments I cut out and where I implemented procedural fluency. I got the activity from Fawn’s blog which you can see: Vroom Vroom. The difference between this post and Fawn’s is initial activity, as well as the need to bring in a Desmos activity builder since they had never used a trend line to make a prediction yet.
Pro tip: This will go over several days, so if you have cars that look alike do not forget to number them!
Vroom Vroom is a lesson using pull back cars from Fawn. Check the link for her implementation. The premise of her lesson is that kids get a pull back car and placed in a competition for who can get their car closet to the finish line. At first they just get the car but do not know how far away the finish line is going to be and so collect data about how far the car travels from various pull back distances. Then armed with just their data and regression, the are told how far away the finish line is going to be and they must decide how far they are going to pull back the car. Closest wins. I did do that same thing, but not until day 3.
My implementation is different because I also wanted to use it as a vehicle for an introduction to statistics.
Day 1: Collecting Data From A Single Distance
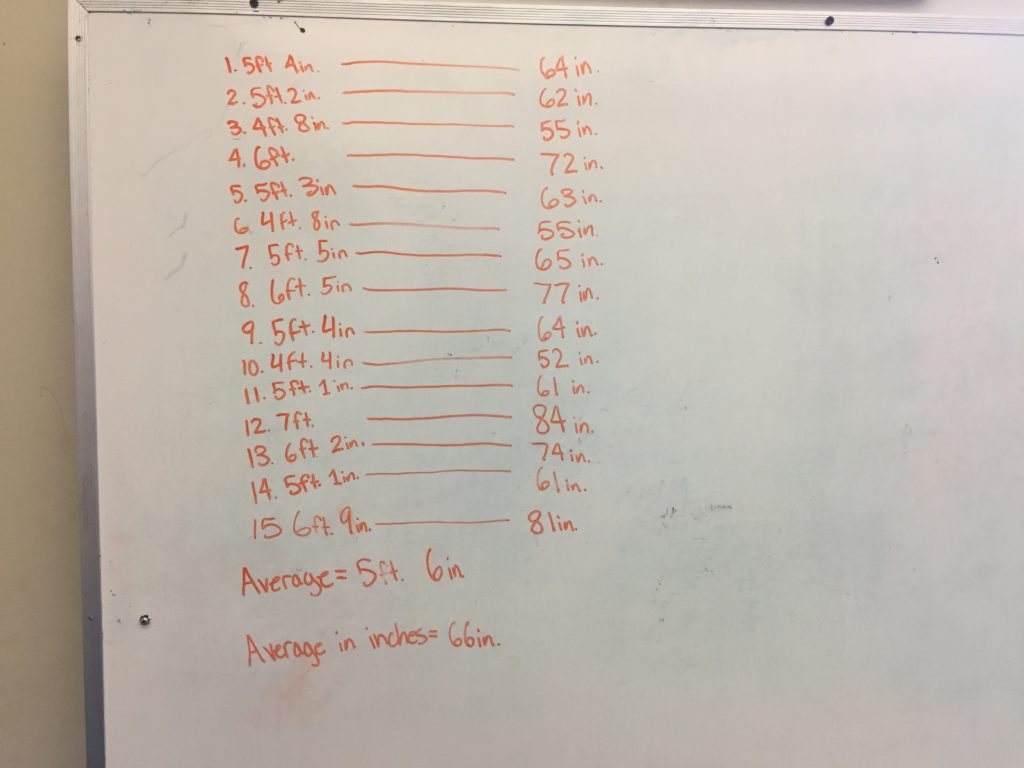
I told the kids that they (groups of 3) were going to get a pull back and I wanted them to take 15 measurements of how far the car travels when pulled back 5 inches. I gave them time to discuss and decide if they needed any clarification. These are the types of questions I got:
- Do we measure from the starting line of from the release point? (my answer was starting line)
- What do we do if it doesn’t go straight? (still measure how far it went. Try your best to point it straight and if it doesn’t go perfectly straight then that’s just an attribute of your car)
- When it’s done moving, do we measure it from the front of the car to the finish line? (yes)
- Do we put the front wheels on the starting line or the front of the car? (front of car)
Teacher Move I Needed:
- After the first couple measurements I got the class’s attention and reminded them not always have the same person measure. Learning how to measure the distances to the nearest quarter inch was one of learning goals and everyone should take turns doing it. It seemed like each group had given themselves roles – pull back person, measure person, and recorder person. I didn’t want that.
The reason I didn’t start with the competition was that I didn’t think they would have a natural sense of the variability of the cars performance. By beginning this way I believe they will do a better job with the competition data collection. We’ll see tomorrow.
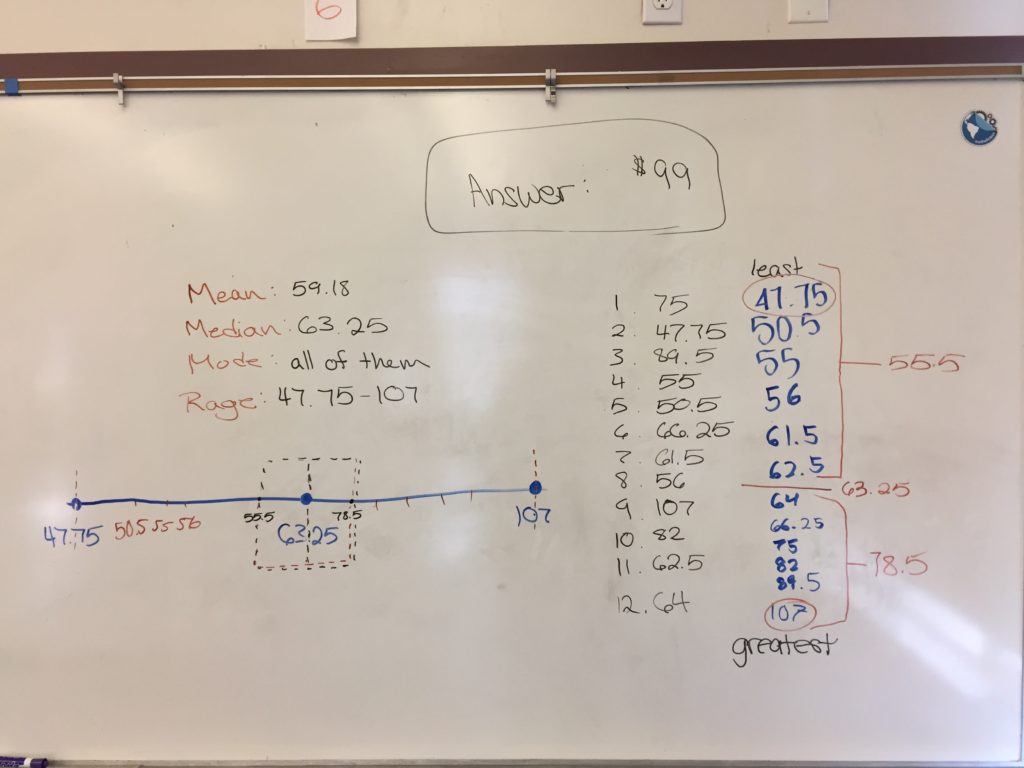
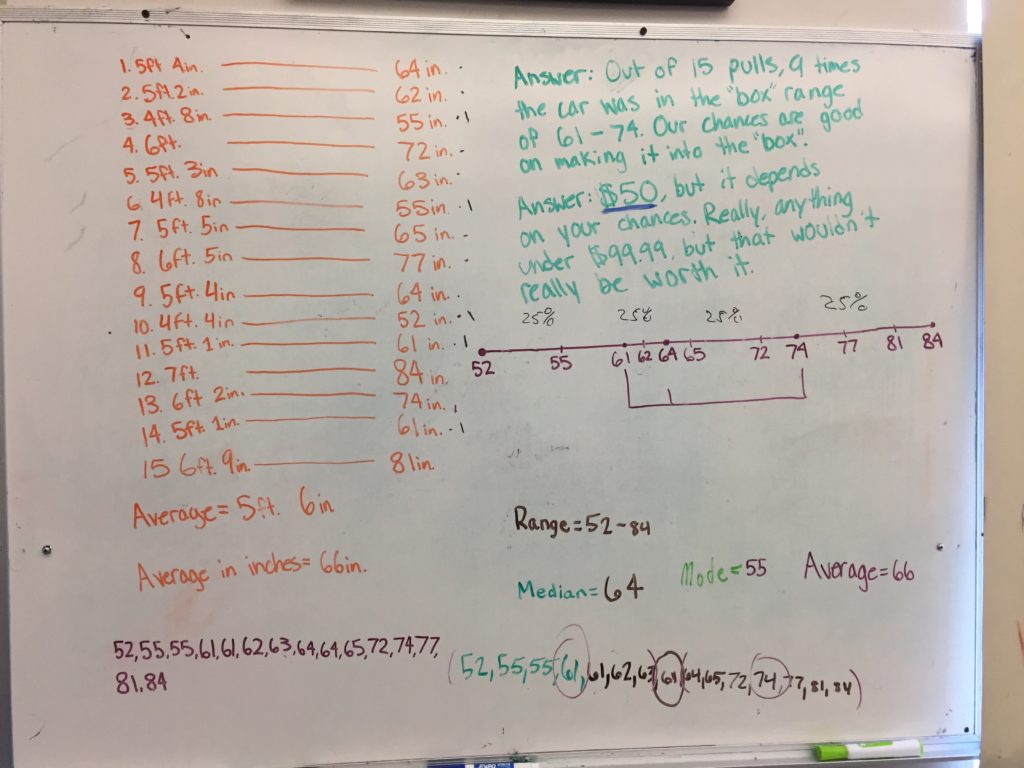
At this point I decided to give a mini lesson of how to find range, mean, median, and mode. I showed them how to do it and gave them a worksheet for practice. Initially the students worked “alone” (told to put on headphones or ear plugs and no talking or questions) When they were sufficiently far I had them go back to their whiteboards and find the mean, range, median, and mode of their data set and graph the numbers on the number line.
Then told them how to make a box plot of the data
Thinking Questions: Here are some great questions to get the students thinking. I always recommend teachers come up with these types of questions and turn them into “talking points” – it’s the best way I know to get everyone one record and discussing.
- How confident are you that if you try it again the distance the car travels will be in the box?
- If the prize for having the car end up in the box was $100, how much would you be willing to spend to play the game?
- Is the mean or median the most appropriate measure to base our predictions on.
- Let’s say you pulled the car back one more time and by some act of God it went 25000 inches. What would your new mean and median be?
The final part of this day the students pull their car back one last time and see if it falls within their box. I tell them to imagine they actually made the best, that money was on the line. Once back to their seats we reflected on the activity and possible sources of error.
I should add that during the reflection I asked them how confident they would have been if I said the car had to travel anywhere between 0ft and 300ft. They were 100% confident. I used that to tell them informally about the 95% confidence interval.
Day 2 The Competition Begins
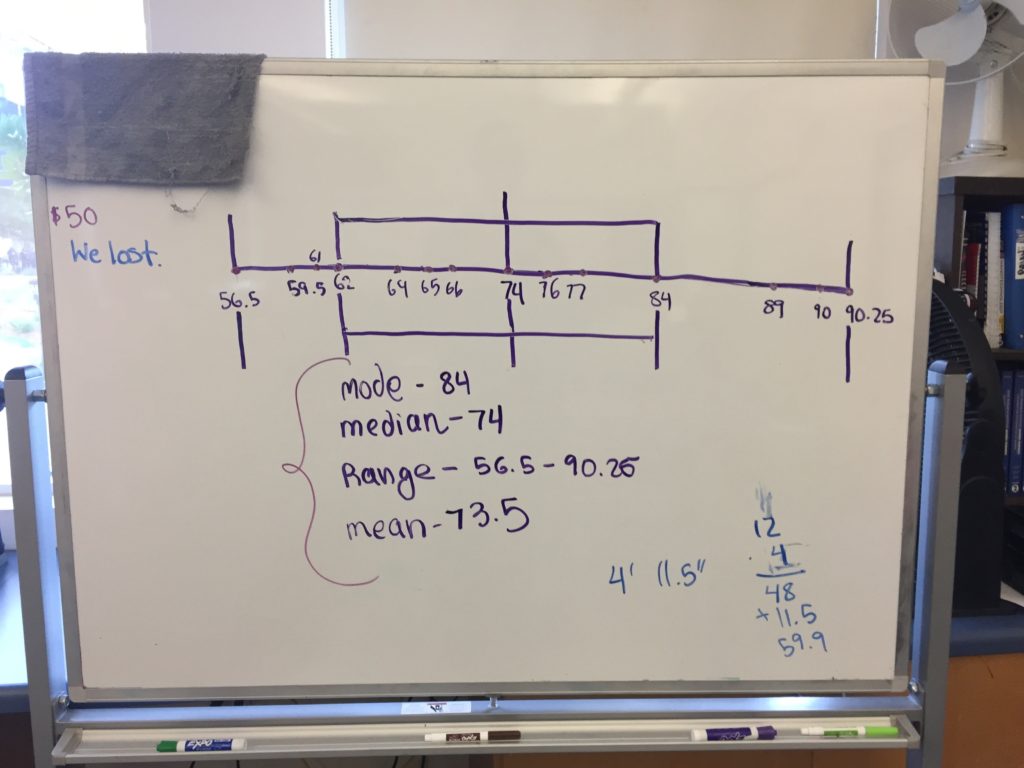
Today I tell them that they are in a competition. Which ever group gets closest to the finish line wins. They get 20 minutes with their car. The catch is that they don’t know where the finish line is going to be until after the 20 minutes. At which point they need to decide how far they are going to pull back their car to achieve the proper distance. One chance.
I gave them 2 minutes at the beginning to write up some thoughts on what they are going to do once they have the car. I was able to learn that some students were planning to pull it back as far as it would go. They had not connected to the activity and thought they were suppose to make the car go back as far as possible. Here’s some of the data that was collected:
As teams began to finish I had them begin to enter their data into Desmos. Then I collected the cars and told them the distance was 5′ and they had to come up with a pull back distance.
Day 2 Line Of Best Fit Procedural Fluency
This lesson marked the first time my students used a line of best fit, so I didn’t feel they would be able to use it to help them make their predictions yet. I decided to scaffold that by created an activity in Desmos activity builder. I walked them through the first 3 screens, and they finished it on their own. Then I had them go back and use their new skill to help them make another prediction for the pull back distance. They would be able to test both distances.
Here’s the link to my activity:
https://teacher.desmos.com/activitybuilder/custom/58766a9dd249218510eee439
I used real-world climate data off the EPA’s website. I wanted to have this learning segment to be a conversation that mattered and top of being fun and playing with pull-back cars.
After the students finished the line of best fit Desmos activity I had them use their new skill on the data they collected from the previous day. They each did a line of best fit and got their second estimation for the pull back length.
Day 3
With their estimations in hand – we setup the track and did the competition. The champ got pretty close.
Day 4
I didn’t plan on this day, but the Desmos activity highlighted that the students where unable to describe what the slope of the line of best fit meant in the context of the question. So I handed out two of the graphs from the Desmos activity and taped them to whiteboards and asked the following questions:
The high exit question – which I delivered orally – was to ask them what does the line of best fit predict for year 0? And if they thought it was reasonable to use our line of best fit for a prediction about year 0. We discussed domain and how it’s probably not best to use this post industrial revolution data as a predictor for before the industrial revolution.
I ended with them doing some worksheets “alone” (wearing headphones or ear plugs, no talking, must write questions on a paper) and then “individually” (able to talk to neighbors).
In Retrospect:
Here’s what I didn’t do well:
- Having students keep a written or digital record of the activity. Since it went over several days and was done a lot at whiteboards and on Desmos, there wasn’t much official to turn in.
- Similar to above – but having a more official paper for them to write they group members, car number, daily reflections, and so forth.
- Although they dealt with the repeatability issues in the first activity, I didn’t really go back to that idea and discuss what is the optimum number of measurements for the challenge.
- I wanted to cut out more alone time.
- My students mostly were unable to think consider the nature of the relationship. They tended to assume linear and go with it. I clearly did not do a good enough job last semester having them contrast the different relationships – linear, exponential, quadratic, other.
Conclusion:
I’m happy. I think the goal was achieved of having them understand what a line of best fit is and how to use it to make decisions. Next year it will be better thought. And there will be a next year with this one.
Cheers!
-B