This post is about two new additions to way I taught Robert Kaplinsky’s Ms Pac Man lesson and I recommend them because they made the experience in my class even better (and it was already one of my favorites). I wrote about the lesson previously here. And Deb Boden wrote about it here.
New Addition #1 – Conditions for the double move
I thought of this the day before I did the lesson and I was excited about it – but I didn’t even realize the two improvements it would lead to (namely providing strategy to the game, and providing a way for students to check their solutions).
Here’s what I did: After a few students start to run into that first corner where Ms. Pac Man needs to do more that just rotate – I still waited for a critical mass and then grouped students and had them navigate that turn together at whiteboards.
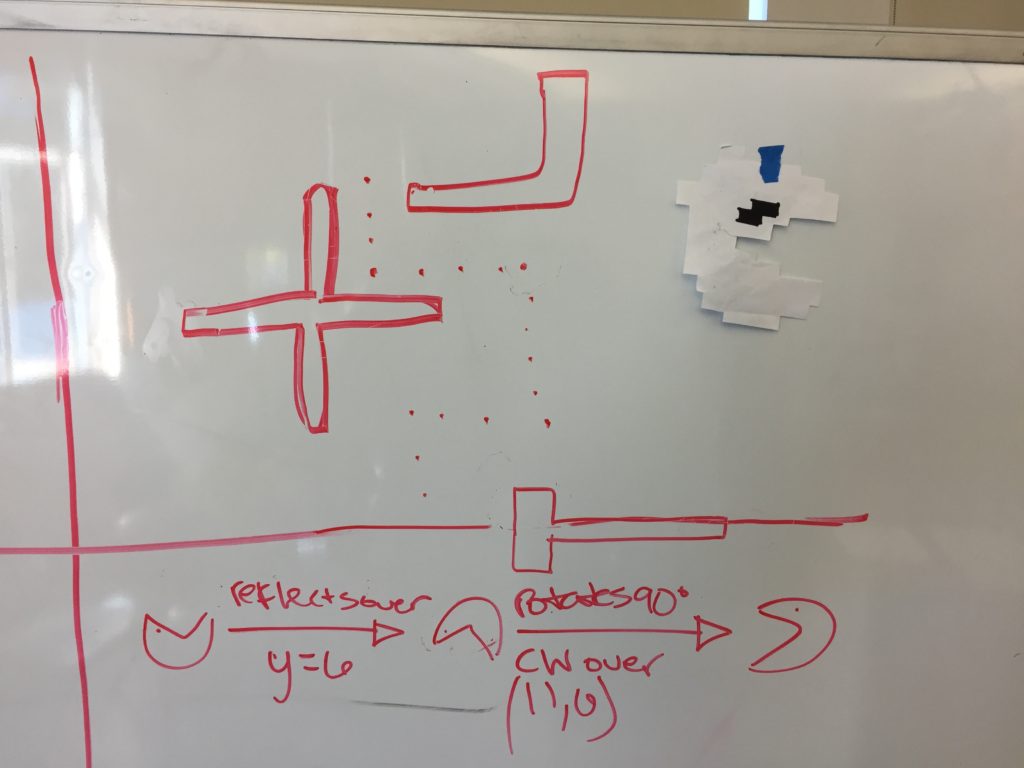
But when they sat back down I hit them with this challenge (which is the new element):
“Find other conditions for a double move”
We had established that if she is moving up and wants to go left that she will need to do more than just rotate. When else will this be true? I gave them about 10 minutes of alone time and after that had a class discussion.
You will have students who don’t feel comfortable enough with the transformations to handle a question like “Find other conditions for a double move”. If I saw students not progressing, I would walk by them and something like “If she is moving left and wants to go down, will this need to be a double move?”. Then come back to them and ask “What other times will she need to do a double move?”
Turns out that every left turn and every turn when she is moving left will require two moves. There are two reasons why that is a great discovery from the lesson perspective:
#1: Now when they play the game to score the most possible points in 20 moves they can have a strategy. Minimize these moves that take two transformations. And they did! This year over half the class was even mapping out their entire path before actually recording the individual moves. They were counting out the moves per turn and trying to minimize the number of left turns. The students recording each move also seem to be doing so with increased strategy.
#2: If you are doing the activity Robert suggests where they figure out all the transformations to complete the path on the screen, you’ll always get some form of this question: “Mr Miller I’m done but I don’t know if it’s right”. Now you can challenge them to count up how many moves it should take based on knowledge of which turns are a double and which are a single. If they used a different number of moves then they probably made a mistake somewhere. This type of self check on the answer helps extend the activity because the early finishers have something to do.
A Subtle Distinction
If you notice in the image above I had written “triple” move instead of double move. That’s because students disagreed on whether they should count the translation as a separate move or not. That happened because one of my students offered the beginning move as a double because it’s a reflection and then a translation. But if that’s a double, then our “double” moves (reflection, rotation) were actually triple (reflection, rotation, translation). This was probably one of the most subtle distinctions that I have had an active group conversation about with my students. Loved. Every. Minute.
New Addition #2 – Draw the resulting orientation of Ms Pac Man after each move.
I got this idea from Alex Wilson and it was very effective. I recommend it highly. Last year I just had them write all the transformations without the additional image of Ms. Pac Man. Have them keep track of Ms Pac Man’s orientation after each move.
I also – mostly in the moment – came up with a way to address a very common mistake without telling them the answer, so here it is:
Anticipation – Here is a way to navigate a common mistake:
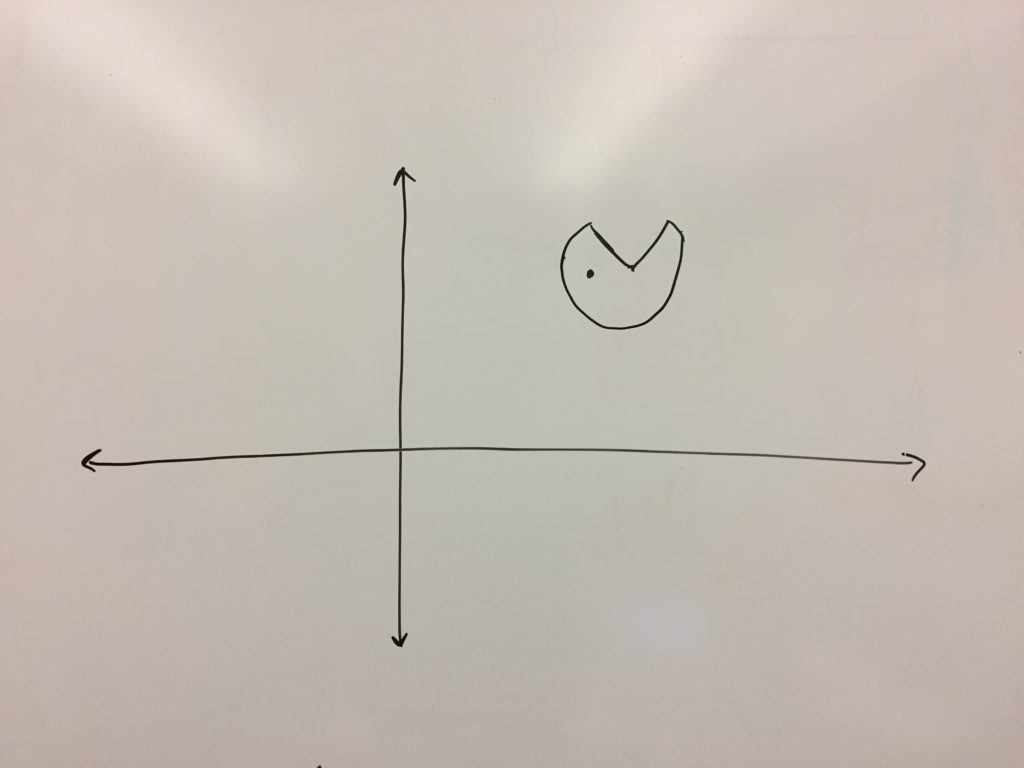
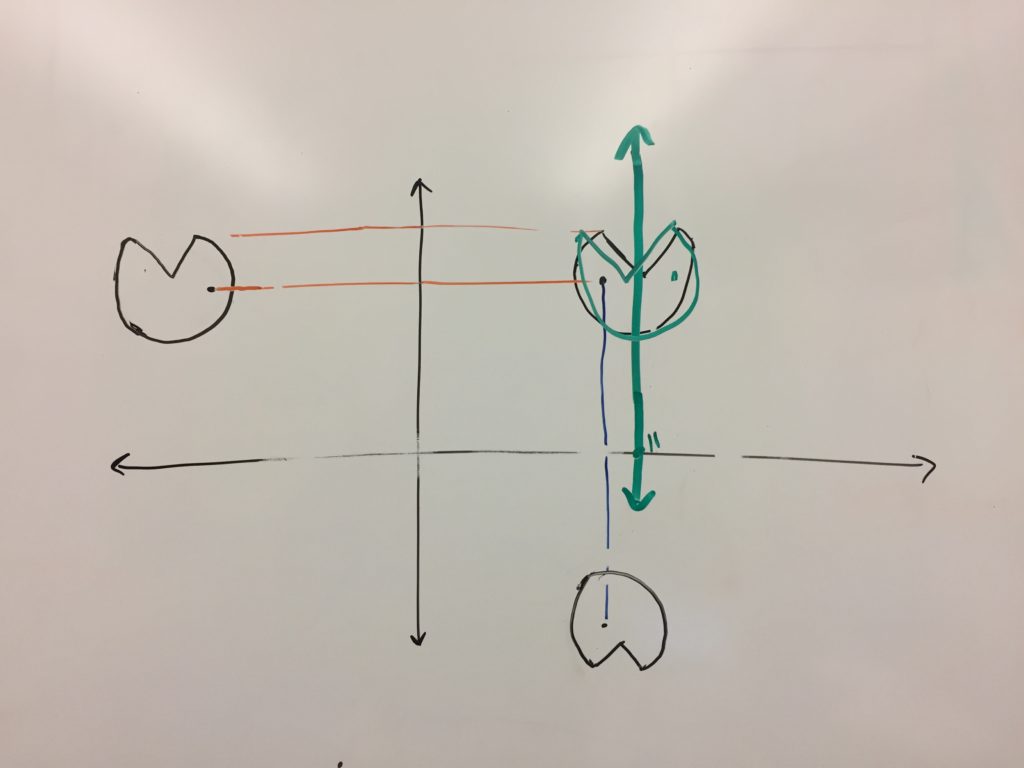
Lastly – I definitely recommend having them say exactly what line they are reflecting over, rather that just vertical or horizontal reflection. And when you do that you are sure to have some student always write “reflect over y-axis” for every vertical reflection, and “reflect over x-axis” for every horizontal reflection (when really they are reflecting over y=h or x=k). So what I did this year after I noticed a critical mass doing that in one of my classes, I asked everyone to sketch an x-y axis and put Ms. Pac Man in the first quadrant. Like so:
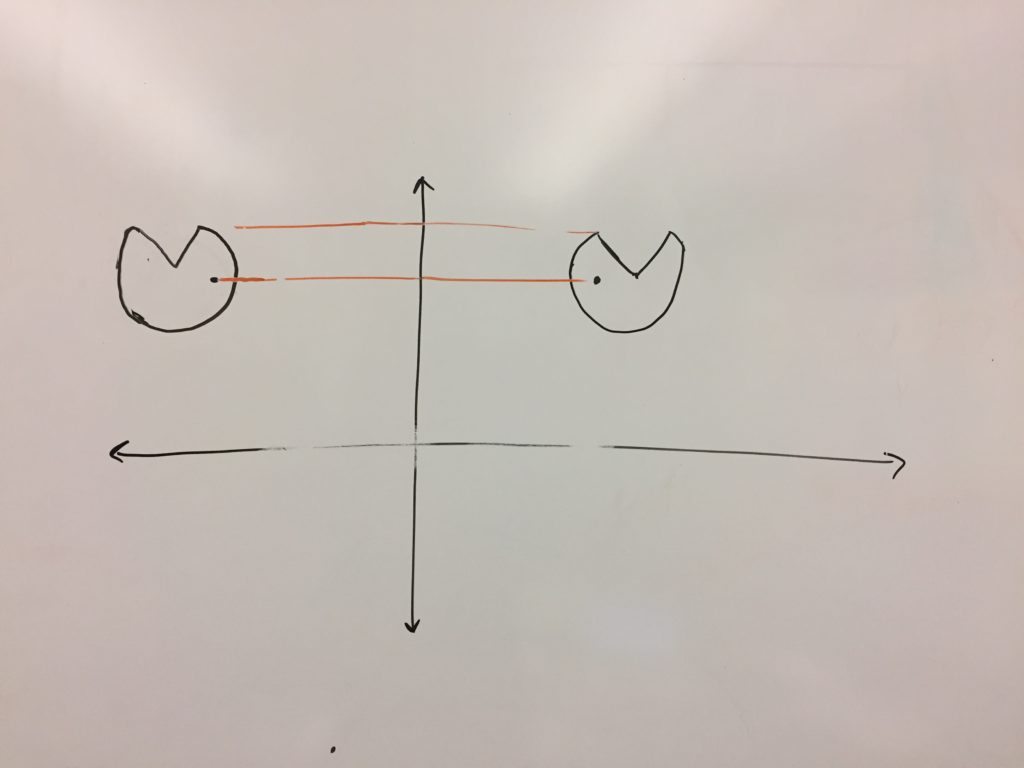
Then I told them to reflect her over the y-axis.
That was pretty much all they needed to see for them to realize that Ms. Pac Man is not reflecting over the y-axis in the game. Then I had them draw a line through Ms Pac Man and reflect her over that line, as well as the x-axis. The next day, and I’m not kidding on this – not a single group of 2 students had her reflecting over the wrong line (although one group had her reflecting over points). Turned out to also be a great spiraling of reflecting shapes.
This post is really about having more in our back pocket as we try provide this learning experience to our students as best we can.
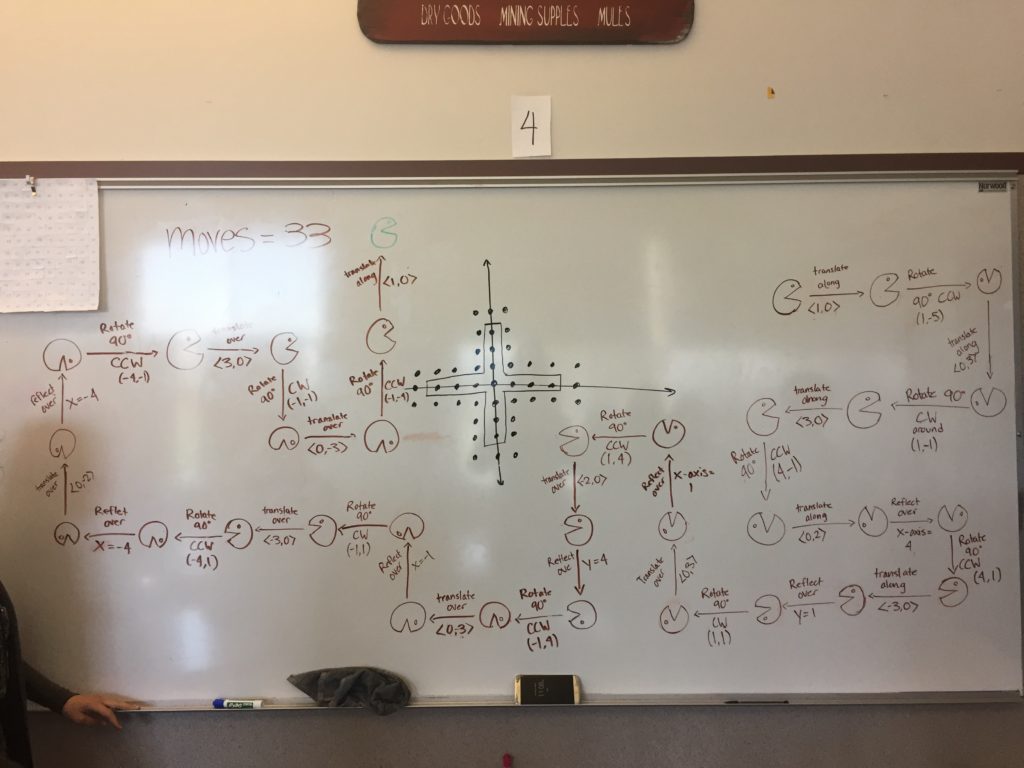
By the way – I did the lesson over two days. I did the opener that I blogged about previously on day 2, where they send Ms Pac Man around the plus sign. Here are 9 of the 12 whiteboards groups I had (that’s the most I can fit on an image)
Cheers!
-B


4 responses to “Adding To Ms Pac Man”